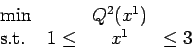
with
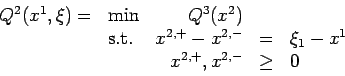
and
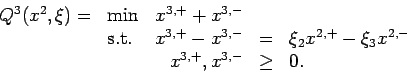
The random variable
Show that the optimal value of this problem is zero, achieved by any feasible x1.
Show that setting each ![]() equal to its mean and solving the resulting problem
does not give a lower bound on Q2(x1), unless x1=2.
equal to its mean and solving the resulting problem
does not give a lower bound on Q2(x1), unless x1=2.
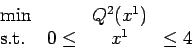
with
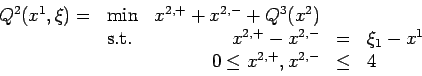
and
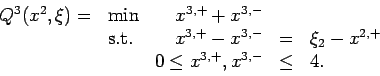
The random variables
By formulating the extensive form of the problem as a linear programming problem, or otherwise, confirm that the optimal value is 2.5. Show that if x1=0 then Q2(x1)=3.
Take x1=2 as the first stage solution in the nested L-shaped method for this problem.
Find the first cut generated by the algorithm of the form
![]() .
Show that
E11x1 + Q2(x1) > e11 for all feasible x1.
.
Show that
E11x1 + Q2(x1) > e11 for all feasible x1.