- (a)
- Show that the second stage problem has six constraints and nine variables, once slacks are included, but that there are only eight bases which need to be considered. What are the corresponding dual optimal solutions?
- (b)
- Solve the problem using the L-shaped method. Take
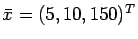 as the first stage variables in the solution to the initial relaxation.
Include the simple bounds that x should be no larger than the maximum
demand.
Also include the simple bounds
that the revenue in any scenario can be no larger than the revenue
obtained from the maximum demand for that scenario.
For example, the maximum possible revenue under Scenario 2 is 255,
normalizing so that the revenue from an economy class passenger is 1.
Use the multicut method.
If there are multiple optimal dual solutions, add all the possible
constraints.
You should get the optimal solution after three rounds of adding cutting
planes.
as the first stage variables in the solution to the initial relaxation.
Include the simple bounds that x should be no larger than the maximum
demand.
Also include the simple bounds
that the revenue in any scenario can be no larger than the revenue
obtained from the maximum demand for that scenario.
For example, the maximum possible revenue under Scenario 2 is 255,
normalizing so that the revenue from an economy class passenger is 1.
Use the multicut method.
If there are multiple optimal dual solutions, add all the possible
constraints.
You should get the optimal solution after three rounds of adding cutting
planes.
![\begin{displaymath}
\begin{array}{rcl}
\left[ \begin{array}{rrrr}1&3&-1&0\\ 2&-1...
...5&-1&0\\ 0&2&4\end{array}\right] x \\
y & \geq & 0
\end{array}\end{displaymath}](img2.gif)
where