Please do all four problems. Show all work. No books or calculators allowed. You may use any result from class, the homeworks, or the texts, except where stated. You may use one sheet of handwritten notes. The exam lasts 110 minutes.

1. (25 points) The linear program min{c^T x : Ax = b,x ≥ 0} has

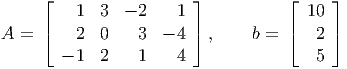
   and the point x^* = (3,2,0,1)^T is an optimal solution.

   1. (5 points) Show x^* is not a basic feasible solution.
   2. (10 points) Find a nonzero direction d ∈ ℝ⁴ satisfying Ad = 0 with d _j = 0 if x_j^* = 0.
   3. (10 points) What can you say about c^T d? Justify your answer.

   Solution:

   1. Row reduce the 3 columns of A used by x^*:

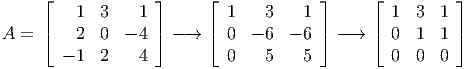
      so the set of columns used by x^* gives a submatrix of A of rank only 2.

   2. We have

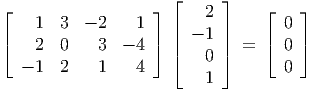
      so we can take d = (2,-1, 0, 1)^T .

   3. We must have c^T d = 0, since both x^* + 2d and x^*- d are feasible, so if c^T d≠0 then one of these two feasible points would be better than x^*, contradicting the optimality of x^*.
2. (25 points)

   A primal LP is

   

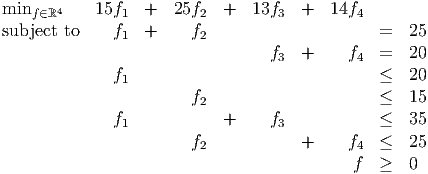
   The corresponding dual problem is

   

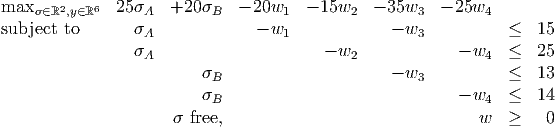
   Find optimal solutions to the primal and dual problems.

   Solution:

   Variable f₁ has far smaller cost than f₂, so we try to make f₁ as large as possible. Similarly, if we have a choice between f₃ and f₄, we would pick f₃. This gives a primal feasible solution:

   

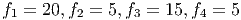
   with value

   

   If we can find a dual feasible solution that satisfies complementary slackness then we have an optimal solution.

   All the primal variables are positive, so we need all four dual constraints to hold at equality. The 2nd and 4th primal inequality constraints are strictly satisfied, so we need w₂ = w₄ = 0. This implies we need

   

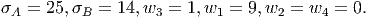
   Since we are primal and dual feasible and we satisfy complementary slackness, we are optimal.

   Check: dual objective function value is

   

3. (30 points; each part is worth 5 points) We have a primal-dual pair of linear programs

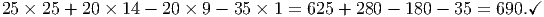
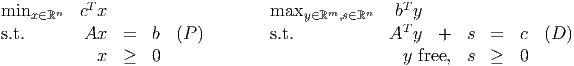
   where the dual slack variables have been included explicitly. Assume both problems are feasible. We let e_j ∈ ℝⁿ denote the jth unit vector. We also work with the related primal-dual pair of problems

   
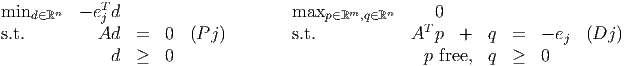
   1. Show that problem (Pj) is always feasible.
   2. Assume (Pj) has an unbounded optimal value. Show x_j is unbounded in the feasible region of (P).
   3. Assume (Pj) has a finite optimal value. What is that optimal value? Can x_j be unbounded in the feasible region of (P)? Why or why not?
   4. Assume (Dj) is feasible. Can s_j be unbounded in the feasible region of (D)? Why or why not?
   5. Assume (Dj) is infeasible. Can s_j be unbounded in the feasible region of (D)? Why or why not?
   6. Show exactly one of the following two statements is true:
      • x_j is unbounded in the feasible region of (P).
      • s_j is unbounded in the feasible region of (D).

   Solution:

   1. Note that d = 0 is always feasible in (Pj).
   2. Since (Pj) has an unbounded optimal value, there must exist a ray d ≥ 0 with -e_j^T d < 0, Ad = 0. Let x be feasible in (P). Then x + αd is feasible in (P) for all α ≥ 0, and we have (x + αd)_j →∞ as α →∞.
   3. (Pj) is a homogeneous problem, so the only possible finite optimal value is 0. For x_j to be unbounded in (P), there must exist a direction d ≥ 0 with d_j > 0, Ad = 0. But no such d exists since (Pj) has optimal value 0.
   4. Let y,s be feasible in (D) and let p,q be feasible in (Dj). Then y = y + αp, s = s + αq + αe_j is feasible in (D) for any α ≥ 0. Note that s_j →∞ as α →∞.
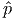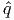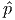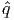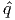   5. For s_j to be unbounded, we need to find a direction , with A^T + = 0, ≥ 0, 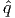_j > 0. We can scale this direction so that 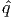_j ≥ 1. Then 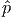, (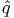- e_j) is feasible in (Dj). If (Dj) is infeasible then no such direction exists, so s_j must be bounded.
   6. There are 2 possible cases for (Pj) since it is always feasible:
      • (Pj) has unbounded optimal value, so (Dj) is infeasible, so in this case we have x_j is unbounded and s_j is bounded.
      • (Pj) has zero optimal value, so (Dj) is feasible, so in this case we have x_j is bounded and s_j is unbounded.
4. (20 points) Consider the semi-infinite linear program

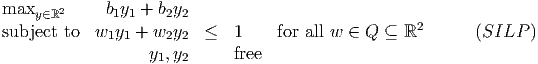
   where we have a constraint for each w ∈ Q, and we define

   

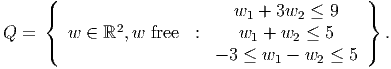
   Derive an equivalent linear program to (SILP) with the same variables y₁, y₂ and with a finite number of constraints.

   Solution:

   We can sketch Q:

   

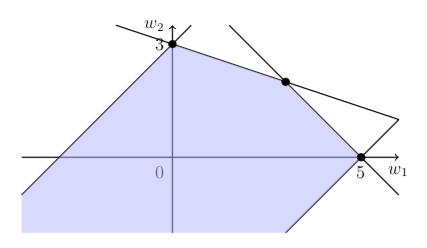
   Any point in Q can be represented as a convex combination of the extreme points plus a nonnegative multiple of the ray:

   

   with λ₁ + λ₂ + λ₃ = 1,λ_j ≥ 0 for j = 1, 2, 3,μ ≥ 0.

   So (SILP) is equivalent to the LP with 4 constraints:

   

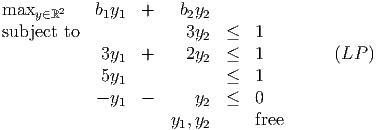
   The feasible region for this LP is as follows:

   

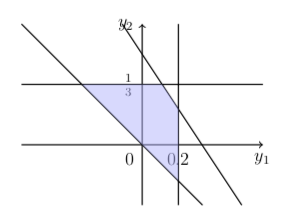
   Note that we have

   

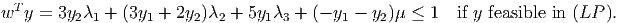
   So if y is feasible in (LP) then it is feasible in (SILP).

   Conversely, if y is not feasible in (LP) then either w^T y > 1 for one of the extreme points of Q, or y₁ + y₂ < 0, which implies w^T y > 1 for w = -t(1, 1)^T ∈ Q for large enough t. So y is not feasible in (SILP).

   Thus the two problems are equivalent.