Name:

MATP6640/ISYE6770
Linear Programming
Spring 2022

Midterm Exam, Friday, March 18, 2022.

Please do all four problems. Show all work. No books or calculators allowed. You may use any result from class, the homeworks, or the texts, except where stated. You may use one sheet of handwritten notes. The exam lasts 110 minutes.

Q1		/25

Q2		/25

Q3		/30

Q4		/20


Total		/100

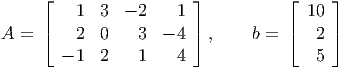
(25 points) The linear program min{c^Tx : Ax = b,x ≥ 0} has $⌊ ⌋ ⌊ ⌋ 1 3 - 2 1 10 A = ⌈ 2 0 3 - 4 ⌉, b = ⌈ 2 ⌉ - 1 2 1 4 5$
and the point x^* = (3,2,0,1)^T is an optimal solution.
1. (5 points) Show x^* is not a basic feasible solution.
2. (10 points) Find a nonzero direction d ∈ ℝ⁴ satisfying Ad = 0 with d_j = 0 if x_j^* = 0.
3. (10 points) What can you say about c^Td? Justify your answer.
(this page intentionally left blank)
(25 points)
A primal LP is
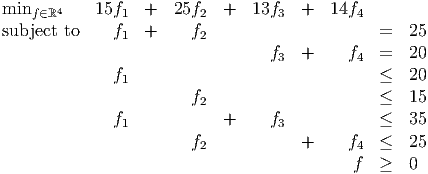
$minf∈ℝ4 15f1 + 25f2 + 13f3 + 14f4 subject to f1 + f2 = 25 f3 + f4 = 20 f1 ≤ 20 f2 ≤ 15 f1 + f3 ≤ 35 f2 + f4 ≤ 25 f ≥ 0$
The corresponding dual problem is
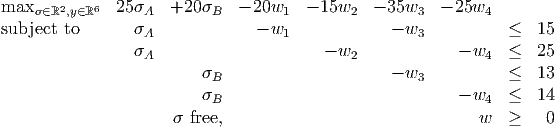
$max σ∈ℝ2,y∈ℝ6 25σA +20 σB - 20w1 - 15w2 - 35w3 - 25w4 subject to σA - w1 - w3 ≤ 15 σA - w2 - w4 ≤ 25 σB - w3 ≤ 13 σB - w4 ≤ 14 σ free, w ≥ 0$
Find optimal solutions to the primal and dual problems.
(this page intentionally left blank)
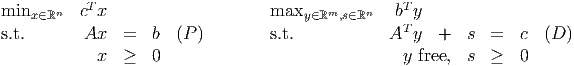
(30 points; each part is worth 5 points) We have a primal-dual pair of linear programs $minx ∈ℝn cTx maxy ∈ℝm,s∈ℝn bTy s.t. Ax = b (P ) s.t. AT y + s = c (D ) x ≥ 0 y free, s ≥ 0$
where the dual slack variables have been included explicitly. Assume both problems are feasible. We let e_j ∈ ℝⁿ denote the jth unit vector. We also work with the related primal-dual pair of problems
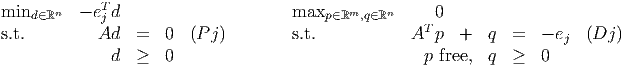
$mind ∈ℝn - eTj d maxp ∈ℝm,q∈ ℝn 0 s.t. Ad = 0 (Pj ) s.t. AT p + q = - ej (Dj ) d ≥ 0 p free, q ≥ 0$
1. Show that problem (Pj) is always feasible.
2. Assume (Pj) has an unbounded optimal value. Show x_j is unbounded in the feasible region of (P).
3. Assume (Pj) has a finite optimal value. What is that optimal value? Can x_j be unbounded in the feasible region of (P)? Why or why not?
4. Assume (Dj) is feasible. Can s_j be unbounded in the feasible region of (D)? Why or why not?
5. Assume (Dj) is infeasible. Can s_j be unbounded in the feasible region of (D)? Why or why not?
6. Show exactly one of the following two statements is true:
  - x_j is unbounded in the feasible region of (P).
  - s_j is unbounded in the feasible region of (D).
(this page intentionally left blank)
(this page intentionally left blank)
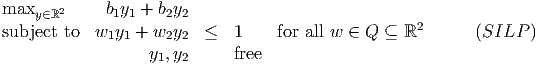
(20 points) Consider the semi-infinite linear program $maxy ∈ℝ2 b1y1 + b2y2 subject to w y + w y ≤ 1 for all w ∈ Q ⊆ ℝ2 (SILP ) 1 1 2 2 y1,y2 free$
where we have a constraint for each w ∈ Q, and we define
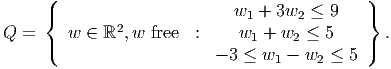
$( w + 3w ≤ 9 ) { 2 1 2 } Q = ( w ∈ ℝ ,w free : w1 + w2 ≤ 5 ) . - 3 ≤ w1 - w2 ≤ 5$
Derive an equivalent linear program to (SILP) with the same variables y₁, y₂ and with a finite number of constraints.
(this page intentionally left blank)