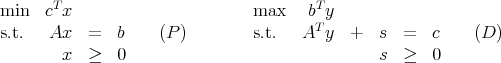
MATP6640/DSES6770
Linear Programming
Spring 2010

Midterm Exam, Tuesday, April 6, 2010.

Please do all three problems. Show all work. No books or calculators allowed. You may use any result from class, the homeworks, or the texts, except where stated. You may use one sheet of handwritten notes. The exam lasts 110 minutes.

Throughout, the standard primal-dual LP pair is

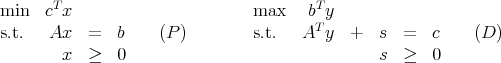
min cTx max bTy s.t. Ax = b (P ) s.t. AT y + s = c (D ) x ≥ 0 s ≥ 0

where A is m × n and the vectors are dimensioned appropriately.

(30 points)
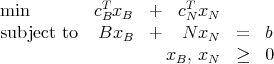
The linear program $min cTxB + cT xN subject to BBx + NN x = b B N xB, xN ≥ 0$
has x_B 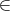IR³, x_N 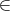IR¹, b 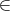IR³, and c, B, and N dimensioned appropriately. The matrix B is invertible, and matrices L and U are known with LB = U, and
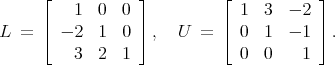
$⌊ 1 0 0 ⌋ ⌊ 1 3 - 2 ⌋ | | | | L = ⌈ - 2 1 0 ⌉, U = ⌈ 0 1 - 1 ⌉ . 3 2 1 0 0 1$
Let
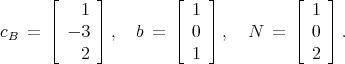
$⌊ ⌋ ⌊ ⌋ ⌊ ⌋ | 1 | | 1 | | 1 | cB = ⌈ - 3 ⌉, b = ⌈ 0 ⌉, N = ⌈ 0 ⌉. 2 1 2$
Solve the following questions without finding B explicitly.
1. (10 points) Show that the basic feasible solution for basis B has x_B = (3, 2, 4)^T.
2. (10 points) Use complementary slackness to show that the corresponding dual solution is y = (7,-10,-2)^T.
3. (10 points) For what values of c_N is this solution optimal?
(30 points)
A set of exams {1,…,n} is to be given, with only one exam given at a time. Exam i has duration l_i and a day has length L. An exam must start and finish on the same day. It is desired to schedule the exams in as few days as possible. Let S^j ⊆{1,…,n} be a set of exams that can be scheduled in a single day and let a_j IRⁿ be the incidence vector of this set. Each set S^j must observe the restriction that no student sits more than one exam in a single day. This restriction can be modeled using a set of pairs P of exams, with (p,q) P corresponding to at least one student taking both exams p and q.
1. (10 points)
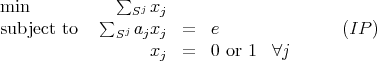
  Show that the problem can be modeled as the following integer program: $min ∑ j x ∑ S j subject to Sj ajxj = e (IP ) xj = 0 or 1 ∀j$
  where the sum is taken over all valid subsets S^j ⊆{1,…,n}, and e denotes the vector of ones.
2. (20 points)
  In a column generation approach to solve the LP relaxation of (IP), a primal solution x and a dual solution y are generated as optimal solutions for the current set of columns. How do you determine whether x and y solve the full LP relaxation?
(10 points)
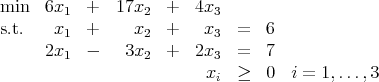
Consider the LP: $min 6x1 + 17x2 + 4x3 s.t. x1 + x2 + x3 = 6 2x1 - 3x2 + 2x3 = 7 x ≥ 0 i = 1,...,3 i$

Show that x = (2, 1, 3) is on the central trajectory for this problem, with x^Ts = 36 for some dual feasible s.
(30 points; each part is worth 10 points.)
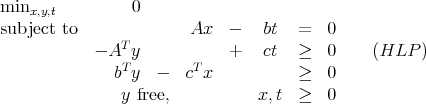
Recall the standard primal-dual pair of linear programming problems (P) and (D) from the cover page. Now consider the linear programming problem $minx,y,t 0 subject to Ax - bt = 0 - AT y + ct ≥ 0 (HLP ) T T b y - c x ≥ 0 y free, x,t ≥ 0$
where t is a scalar.
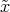1. Suppose the optimal solution to (HLP) is (,ỹ,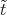 ), with 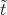> 0. How would you use this solution to find optimal solutions to (P) and (D)?
2. Show that (HLP) is self-dual, that is, the dual to (HLP) is again the problem (HLP).
3. Let (x,y,t) be a solution to both (HLP) and its dual that is strictly complementary and has t = 0. Show that either there exists a vector x ≥ 0 with Ax = 0 and c^Tx < 0 or there exists a vector y with A^Ty ≤ 0 and b^Ty > 0. What can you conclude about (P) and (D)?