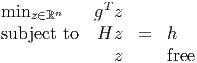Please do all four problems. Show all work. You may use any result from class, the homeworks, or the texts, except where stated.

Scan in a pdf version of your solutions and upload to LMS. You can alternatively write your solutions in LaTeX. Include your name in the name of any file you submit.

I will have WebEx office hours on Thursday from 1-2pm and on Friday from 11am-1pm.

1. (20 points; each point is worth 5 points) Let g ∈ ℝⁿ, h ∈ ℝ^m, and H ∈ ℝ^m×n. Assume rank(H) = m. We look at the LP

   (1)

   1. Is the LP feasible?
   2. Express the LP in an equivalent form min{c^T x : Ax = b,x ≥ 0}. Show that if this problem has a finite optimal value then it has an unbounded set of optimal solutions.
   3. The dual problem is then max{b^T y : A^T y ≤ c}. Does there exist a feasible dual solution y with (A^T y) _i < c_i for some component i?
   4. What must g, h, and H satisfy for (1) to have a finite optimal value? What can you say about the set of optimal solutions to (1) in this case?
2. (20 points) The stochastic program

   (2)

   has second stage cost

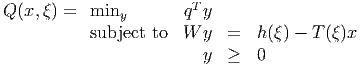   (3)

   Assume all matrices and vectors are dimensioned appropriately. In class, we discussed solving (2) using the L-shaped decomposition method. In class, we only considered the case where the problem has complete recourse, so the second stage problem (3) is feasible for any x feasible in (2).

   How can the method be modified if the assumption of complete recourse does not hold? (Assume the dual LP to the subproblem (3) is feasible.)

3. (20 points) The ampl model file midterm20q3.mod and run file midterm20q3.run generate a random feasible linear program of the form

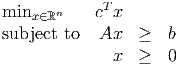   (4)

   with m = 10 and n = 30. The seed is contained in the data file, so choose a random seed and generate an LP. Note that c_j = 1 for all j, and b_i = ∑ _j=1ⁿ(A _ij - 1) for all i. We consider the robust LP model

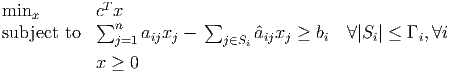   (5)

   where â_ij = 1 for all i, j, and Γ_i = 15 for all i = 1,…, 10. Solve (5). In addition to your optimal x and optimal value, submit your seed, and also submit a data file containing A.

   Note: You don’t need to use AMPL to solve the robust problem, you’re welcome to use a different LP solver. You will need to run AMPL to generate the data file using the command

   ampl: model midterm20q3.run;

   This command will display the A matrix, which you could copy and paste into another solver. The run command also generates a data file containing A, which you can email to me: please put your name in the title of the file.

   (If you don’t even want to use AMPL to generate the data, ensure you generate an instance in the same way, and submit your A matrix using exactly the formatting indicated in the run file.)

4. (40 points. Parts (a)–(f) are worth 5 points each, part (g) is worth 10 points.) Consider the standard form linear program

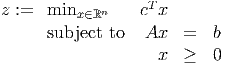   (6)

   where A ∈ ℝ^m×n and rank(A) = m, and b and c are dimensioned appropriately and c has at least one nonzero component. For any nonnegative scalar parameters μ and ν, we can set up a relaxation of (6):

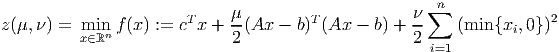   (7)

   1. Show that the optimal value of (7) provides a lower bound for the optimal value of (6).
   2. Let 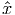be an optimal solution to (7). Show that c^T 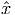< z, the optimal value for (6).
   3. The function f(x) is convex and differentiable with gradient

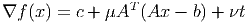
      (8)

      where

      

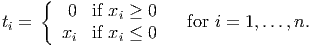
      Any minimizer of f(x) must satisfy ∇f(x) = 0. Show that if x is a minimizer of f(x) then x is infeasible in (6).

   4. Let x satisfy ∇f(x) = 0. Construct a dual feasible solution y to (6), and hence find a lower bound z(y) on the optimal value of (6).
   5. Let x be a solution to (6). Express z(μ,ν) in terms of c^T x and z(y) from part 4d.
   6. Let x minimize f(x). We have constructed three lower bounds on the optimal value of 6, namely c^T x, f(x), and z(y). Which one of these is largest?
   7. Solve 7 for the LP

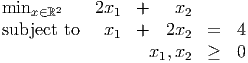
      for a generic μ > 0, ν > 0. What is the dual solution you obtain using the construction of part 4d? (Hint: the optimal solution has x₁ < 0, x₂ > 0.)