Please do all three problems. Show all work. No books or calculators allowed. You may use any result from class, the homeworks, or the texts, except where stated. You may use one sheet of handwritten notes. The exam lasts 110 minutes.

1. (45 points) We have a two stage stochastic program where the nonnegative first stage variables x ∈ ℝ² must satisfy x ₁ + 3x₂ = 6. The first stage costs are c^T x = 2x ₁ + 7x₂. There are two scenarios.
   • Scenario 1 occurs with probability 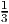. The second stage variable y ∈ ℝ must satisfy the constraints

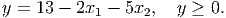
   • Scenario 2 occurs with probability 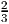. The second stage variable y ∈ ℝ must satisfy the constraints

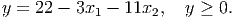
   1. (10 points) Assume x satisfies the first stage constraints. Show that in each scenario, there exists a recourse decision y that is feasible in the second stage problem.
   2. (10 points) Assume the cost of the second stage variables is 3y. Formulate the stochastic program in extended form as an LP. (Hint: your problem should have three equality constraints and four variables.)
   3. (10 points) Find all the basic feasible solutions to the LP formulation. Find the optimal solution.
   4. (5 points) What is the dual to the LP formulation?
   5. (10 points) Use complementary slackness to find the set of optimal solutions to the dual problem.

   Solution:

   1. • In Scenario 1: y = 13 - 2x₁ - 5x₂ ≥ 13 - 2x₁ - 6x₂ = 1, so y ≥ 0.
      • In Scenario 2: y = 22 - 3x₁ - 11x₂ ≥ 22 -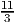x₁ - 11x₂ = 0, so y ≥ 0.
   2. Stochastic program is:

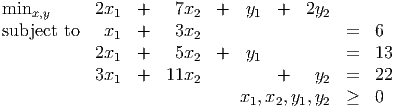
   3. We know from a homework question that this problem has at most two extreme points. The extreme points are found by setting x₁ = 0 or x₂ = 0. They are:
      • x = (0, 2), y = (3, 0), with value 17.
      • x = (6, 0), y = (1, 4), with value 21.

      Hence, the optimal solution is x = (0, 2), with recourse variables y = (3, 0).

   4. Dual problem is

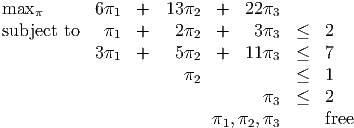
   5. The optimal primal solution is degenerate, so there may be multiple optimal dual solutions. From complementary slackness and dual feasibility, we need:

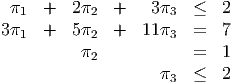
      We can use the two equalities to set π₂ = 1 and then express π₁ = 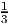(2 - 11π₃). The two inequalities then become:

      
      or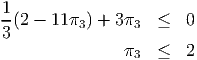

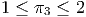
      Thus, the set of dual optimal solutions is the line segment:

      

2. (20 points) Let A be a real p × n matrix and B be a real q × n matrix, with p, q, and n all positive integers. Show that exactly one of the following systems has a solution:

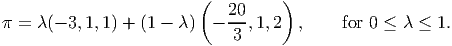
   System 1: Ax < 0, Bx = 0 for some x ∈ ℝⁿ.
   System 2: A^T u + B^T v = 0 for some u ∈ ℝ^p, v ∈ ℝ^q, with u ≥ 0 and u≠0.

   Solution:

   Let e denote the vector of ones. Consider the primal-dual pair of LPs:

   
   1. Assume System 1 is consistent: Any feasible solution to System 1 can be scaled to give a feasible solution to (P). Thus, the optimal value of (P) is 0, so (D) has optimal value 0, so System 2 is inconsistent.
   2. Assume System 1 is inconsistent: Then (P) is infeasible. Problem (D) is always feasible: take u = 0 and v = 0. Thus, (D) must have unbounded optimal value. So there exists u, v with A^T u + B^T v = 0, u ≥ 0, e^T u > 0, so System 2 is consistent.
3. (35 points) In a vehicle routing problem, a set of cities {1,…,n} must be visited, starting from a base city 0. More than one vehicle can be used, with each vehicle traversing a subtour that starts and ends at the base but only visits a subset of the cities. This problem can be formulated as an integer program with each variable corresponding to an allowable subtour. Let T be the set of allowable subtours. Let c_t be the cost of subtour t ∈ T. Let a^t ∈{0, 1}ⁿ be the incidence vector of subtour t ∈ T, so a_i^t = 1 if and only if tour t visits city i for i ∈{1,…,n}. The LP relaxation of the vehicle routing problem can then be expressed as

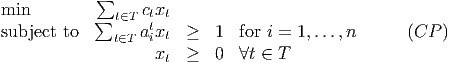
   Let n = 4. Assume the cost c_t of a tour is given by the sum of the edge lengths in the tour, and the edge lengths are as follows:

   city	0	1	2	3	4
   0	–	4	7	9	4
   1	4	–	4	6	8
   2	7	4	–	7	5
   3	9	6	7	–	7
   4	4	8	5	7	–

   

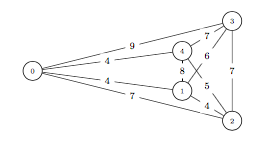
   No tour is allowed to visit more than three cities (plus the base city). A tour can visit just one city and the base city. So, for example, valid tours include 0 - 4 - 0 with cost 8 and 0 - 1 - 2 - 3 - 0 with cost 24.

   1. (5 points) What is the dual LP to (CP)?
   2. (10 points) Let the current dual solution be y = (6, 8, 10, 7)^T . Find a violated dual constraint.
   3. (10 points) There are 14 feasible tours for this problem. Enumerate them all and hence show that ŷ = (4, 8, 12, 5)^T is dual feasible.
   4. (10 points) What does complementary slackness imply about the primal solution if the dual solution is ŷ? Show there is a primal feasible solution satisfying complementary slackness with each positive x_t taking the same value. What do you conclude?

   Solution:

   1. Dual problem is

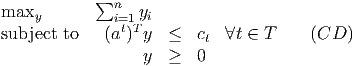
   2. Need a subset of the cities with the length c_t smaller than the sum of the y values for the cities in the subset. Take cities {1, 2, 4}. Then c_t = 17, but (a^t)^T y = 21. The violated constraint is

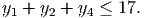
   3. Enumerate the various subsets:

      

      subset t	∑ i∈tyi	ct	(at)T yct
      1	4	8	<
      2	8	14	<
      3	12	18	<
      4	5	8	<
      1,2	12	15	<
      1,3	16	19	<
      1,4	9	16	<
      2,3	20	23	<
      2,4	13	16	<
      3,4	17	20	<
      1,2,3	24	24	=
      1,2,4	17	17	=
      1,3,4	21	21	=
      2,3,4	25	25	=

   4. From complementary slackness, the only primal x_t variables that can be positive are those corresponding to the subsets of size 3. Also, since each ŷ_i > 0, all the primal constraints must hold at equality. So the primal variables must satisfy:

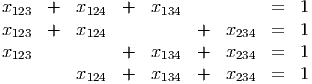
      The solution to this system is x₁₂₃ = x₁₂₄ = x₁₃₄ = x₂₃₄ = 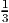, with all other x_t equal to zero. We have primal feasibility, dual feasibility and complementary slackness, so we have optimality.

      Check objective function values:

      • Dual value: 4 + 8 + 12 + 5 = 29.
      • Primal value: 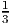(24 + 17 + 21 + 25) = 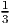(87) = 29.

      So primal and dual objective function values agree.