Please do all three problems. Show all work. No books or calculators allowed. You may use any result from class, the homeworks, or the texts, except where stated. You may use one sheet of handwritten notes. The exam lasts 110 minutes.

1. (30 points; each part is worth 10 points)
   Let A be an n × n matrix satisfying:
   • a_ij ≥ 0 if i≠j, for 1 ≤ i ≤ n and 1 ≤ j ≤ n,
   • and ∑ _i=1ⁿa _ij = 0 for j = 1,…,n.

   Show the following:

   1. Let y ∈ ℝⁿ. Assume the smallest component of y is y _k, so y_k ≤y_i for i = 1,…,n. Show ∑ _i=1ⁿa _iky_i ≥0.
   2. Show the linear program

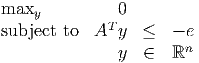
      is infeasible, where e denotes the vector of ones.

   3. What can you say about the set {x ∈ ℝⁿ : Ax = 0,x ≥ 0}?
2. (35 points)
   In the single commodity network flow problem in the figure, nodes s and t are supply nodes and nodes u and v are demand nodes. The supplies available are b_s = 3 and b_t = 2. The demands are d_u = 1 and d_v = 4. The unit shipping costs for each edge are indicated in the figure.

   

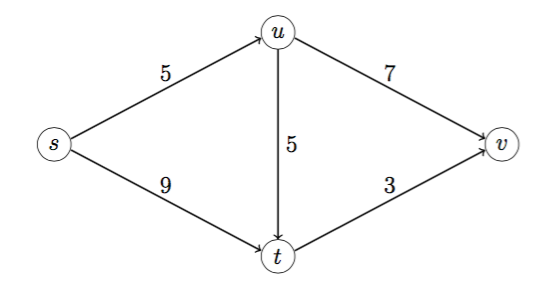
   An initial basic feasible solution can be obtained by taking x_su, x_ut, and x_tv to be basic, and x_st, x_uv to be nonbasic.

   1. (5 points) What is the initial basic feasible solution?
   2. (15 points) What are the primal and dual linear programs? Find a dual solution that satisfies complementary slackness. Show your dual solution is not dual feasible.
   3. (15 points) Make a simplex pivot to improve your primal solution. What is the updated dual solution? Is the new solution optimal?
3. (35 points)
   The numbers on the edges in the following graph represent the probability of failure of an edge. Edges fail independently of one another.

   

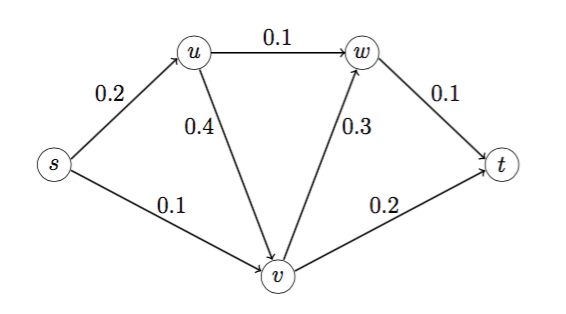
   For a price, we can reinforce an edge so that its probability of failure drops to zero. We want to ensure that a path exists between s and t with high probability. More precisely, we want to ensure that, for each cutset,

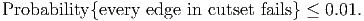   (1)

   A cutset consists of all edges leading from P to Q, where P and Q form a partition of the vertices with s ∈ P and t ∈ Q, so

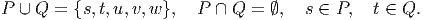   (2)

   Two possible partitions are:

   • P₁ = {s}, Q₁ = {t,u,v,w}. Edges from P₁ to Q₁ are (s,u), (s,v). Probability both edges in the cutset fail is 0.2 × 0.1 = 0.02 ≥ 0.01, so at least one edge in the cutset must be reinforced.
   • P₂ = {s,u,v,w}, Q₂ = {t}. Edges from P₂ to Q₂ are (v,t), (w,t). Probability both edges in the cutset fail is 0.2 × 0.1 = 0.02 ≥ 0.01, so at least one edge in the cutset must be reinforced.

   We introduce variables

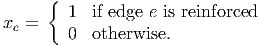   (3)

   In order to ensure the solution x satisfies the constraint (1) for the cutset given by P₁ and Q₁, we can impose the constraint

   

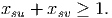
   Similarly, we can impose the constraint

   

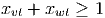
   corresponding to the other cutset. For a general graph, there may be a large number of possible cutsets, so we add the corresponding constraints as needed. The initial LP relaxation is as follows, where the objective function coefficients correspond to the costs of reinforcing a particular edge:

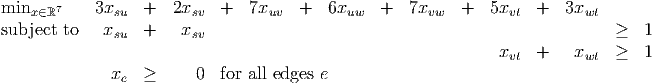   (4)

   1. (5 points) Show that the solution to the initial relaxation is x_sv = x_wt = 1, with all other x_e = 0.
   2. (10 points) Find a cutset that leads to a valid inequality that is violated by the solution in part 3a.
   3. (5 points) Show that x_su = x_wt = 1 with all other x_e = 0 is feasible after the new valid inequality is added to (4).
   4. (15 points) Construct the dual LP to the new problem obtained by adding the constraint to (4). Find a dual solution that satisfies complementary slackness. Is your solution optimal?