Name:

MATP6640/ISYE6770
Linear Programming
Spring 2014

Midterm Exam, Friday, April 11, 2014.

Please do all four problems. Show all work. No books or calculators allowed. You may use any result from class, the homeworks, or the texts, except where stated. You may use one sheet of handwritten notes. The exam lasts 110 minutes.

Q1       /25
Q2       /25
Q3       /25
Q4       /25
Total      /100

Throughout, the standard primal-dual LP pair is

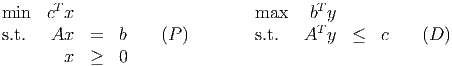
T T min c x max bTy s.t. Ax = b (P ) s.t. A y ≤ c (D ) x ≥ 0

where A is m × n and the vectors are dimensioned appropriately. The rank of the matrix A is m. The dual slack variables are defined as s := c - AT y.

  1. (25 points)
    The problem (P) is
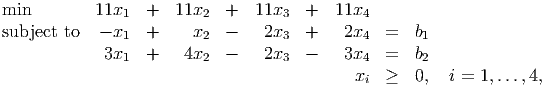
    min 11x + 11x + 11x + 11x 1 2 3 4 subject to - x1 + x2 - 2x3 + 2x4 = b1 3x1 + 4x2 - 2x3 - 3x4 = b2 xi ≥ 0, i = 1,...,4,

    where b1 and b2 are parameters.

    1. (10 points) There is a nondegenerate basic feasible solution to this problem with basic variables x2 and x4. Show that y = (7, 1) is dual optimal.
    2. (15 points) There are other potential columns [ ] a1 a 2 for the matrix A, all with cost c = 11. The corresponding x variables are nonnegative. These additional columns all satisfy the constraints
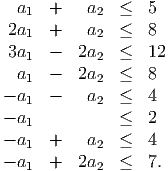
      a1 + a2 ≤ 5 2a1 + a2 ≤ 8 3a1 - 2a2 ≤ 12 a1 - 2a2 ≤ 8 - a - a ≤ 4 1 2 - a1 ≤ 2 - a1 + a2 ≤ 4 - a1 + 2a2 ≤ 7.

      Is the basic feasible solution from part (1a) optimal in the full problem?

    (this page intentionally left blank)

  2. (25 points)
    Let x ∈ IRn be the first stage decision variable in a stochastic program with a finite set S of r scenarios, with the uncertainty represented by ξs, s ∈ S, and with ps equal to the probability of scenario s. We want to minimize the Conditional Value-at-Risk (CVaR) of the second stage decisions, which can be found using the linear program
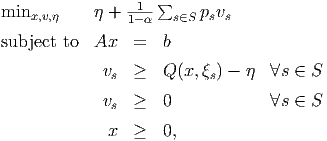    ∑ minx,v,η η + 11-α- s∈S psvs subject to Ax = b v ≥ Q (x,ξ ) - η ∀s ∈ S s s vs ≥ 0 ∀s ∈ S x ≥ 0,
    		(1)

    where α is a parameter, Q(x,ξs) is the recourse cost for the first stage decision x in scenario s, η is a scalar variable, and v ∈ IRr.

    Assume 0 < 1 - α < ps for all s ∈ S.

    1. (15 points) For a fixed x = x, show that the optimal choice for v and η is to take vs = 0 for all s ∈ S and η = max s{Q(x,ξs)}.
    2. (10 points) Hence show that in this case the CVaR problem (1) is equivalent to the robust optimization problem
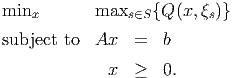
      minx maxs ∈S {Q (x, ξs)} subject to Ax = b x ≥ 0.

    (this page intentionally left blank)

  3. (25 points)
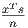    Given a feasible x > 0 for (P) and a feasible (y,s) with s > 0 for (D), let μ = ¯xT¯s n. Let the direction (Δx, Δy, Δz) satisfy the system of equations
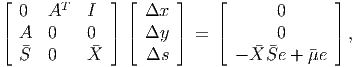
    ⌊ T ⌋ ⌊ ⌋ ⌊ ⌋ | 0 A I | | Δx | | 0 | ⌈ A 0 0 ⌉ ⌈ Δy ⌉ = ⌈ 0 ⌉ , S¯ 0 X¯ Δs - X¯S¯e + ¯μe

    where X and S are diagonal matrices with Xii = xi and Sii = si for i = 1,…,n. Let α be a step length and update

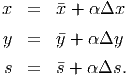
    x = ¯x + α Δx y = ¯y + α Δy s = ¯s + αΔs.

    Show that xT s = nμ.

  4. (25 points.)
    Assume there exists a nonzero direction d ∈ IRm with bT d = 0 and AT d ≤ 0.

    (Hint: You will need to exploit the fact that rank(A) = m in this question. Equivalently, the rows of A are linearly independent.)

    1. (10 points) Show there does not exist a strictly positive x ∈ IRn satisfying Ax = b. What relevance does this have to the application of an interior point method for solving (P) and (D)?
    2. (15 points) Show that every primal optimal basic feasible solution is degenerate.

    (this page intentionally left blank)