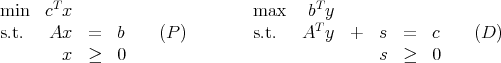
| Name: |
MATP6640/DSES6770
Linear Programming
Spring 2008
Midterm Exam, Thursday, April 3, 2008.
Please do all three problems. Show all work. No books or calculators allowed. You may use any result from class, the homeworks, or the texts, except where stated. You may use one sheet of handwritten notes. The exam lasts 110 minutes.
| Q1 | /40 | |
| Q2 | /30 | |
| Q3 | /30 | |
| Total | /100 |
Throughout, the standard primal-dual LP pair is
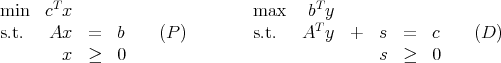
where A is m × n and the vectors are dimensioned appropriately.
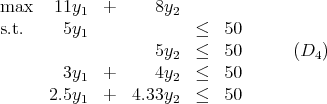
(Hint: 2.5 × 10 + 4.33 × 5 = 46.65.)
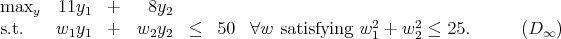
Show that y = (10, 5) is not feasible in the true problem. Give a valid linear constraint that is violated by y = (10, 5) and that could be added to (D4).
(this page intentionally left blank)
(this page intentionally left blank)
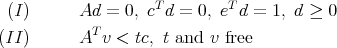
(this page intentionally left blank)
 ,ŷ,ŝ) be strictly feasible solutions to (P) and (D). Let
,ŷ,ŝ) be strictly feasible solutions to (P) and (D). Let  =
=  T ŝ∕n. Assume the current
iterate is reasonably well centered, so
T ŝ∕n. Assume the current
iterate is reasonably well centered, so 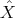 Ŝe ≈
Ŝe ≈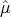 e, with the diagonal matrices
e, with the diagonal matrices 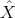 and Ŝ defined
in the usual manner. Assume rank(A) = m.
and Ŝ defined
in the usual manner. Assume rank(A) = m.
Assume we add an extra variable w to (P), with corresponding column g, giving the modified problem
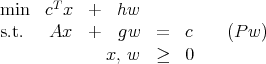
where h is a scalar. The point x = 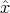 , w = 0 is feasible for (Pw) but not strictly feasible. It is
necessary to increase w to get a strictly feasible point.
, w = 0 is feasible for (Pw) but not strictly feasible. It is
necessary to increase w to get a strictly feasible point.
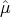 e? (Hint: set
up conditions to be satisfied by primal directions (Δx, Δw) and dual directions
(Δy, Δs).)
e? (Hint: set
up conditions to be satisfied by primal directions (Δx, Δw) and dual directions
(Δy, Δs).)
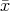 ,
,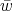 ) and
a new dual solution
) and
a new dual solution 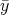 with
with 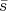 = c - AT
= c - AT 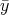 > 0. If you could pick the scalar h, how
would you select it? (Aside: an algorithm could work from an incorrect h and
gradually modify it to achieve the correct value.)
> 0. If you could pick the scalar h, how
would you select it? (Aside: an algorithm could work from an incorrect h and
gradually modify it to achieve the correct value.)(this page intentionally left blank)