MATP6640/DSES6770 Linear Programming, Homework 6.

Due: 11.59pm on Tuesday, April 23, 2024 on LMS.
10% penalty for each day late.

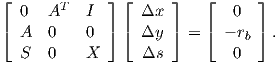
Let (Δx,Δy,Δs) solve $⌊ ⌋ ⌊ ⌋ ⌊ ⌋ 0 AT I Δx 0 ⌈ A 0 0 ⌉ ⌈ Δy ⌉ = ⌈ - rb ⌉. S 0 X Δs 0$
Assume r_b≠0, S and X are positive definite diagonal matrices, and A is m×n with rank m. Show that Δx^TΔs≠0.
Let K be a cone. A function f : int(K) → ℝ is logarithmically homogeneous if there exists a constant Θ such that f(tx) = f(x) - Θln(t) for all x ∈ int(K) and t > 0. (Here, int(K) denotes the interior of K.) Show that the barrier function for the second order cone, namely f(x) = -ln(x₁² -∑ _i=2ⁿx_i²), is logarithmically homogeneous, where ξ is a nonnegative scalar, x is an n-vector, and K = {x : ∑ _i=2ⁿx_i² ≤ x₁²}. What is the value of Θ?
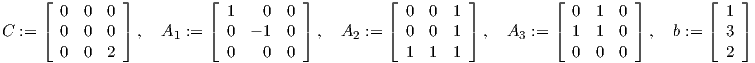
Let $⌊ 0 0 0 ⌋ ⌊ 1 0 0 ⌋ ⌊ 0 0 1 ⌋ ⌊ 0 1 0 ⌋ ⌊ 1 ⌋ C := ⌈ 0 0 0 ⌉ , A := ⌈ 0 - 1 0 ⌉, A := ⌈ 0 0 1 ⌉, A := ⌈ 1 1 0 ⌉ , b := ⌈ 3 ⌉ 1 2 3 0 0 2 0 0 0 1 1 1 0 0 0 2$
The primal and dual semidefinite programs are
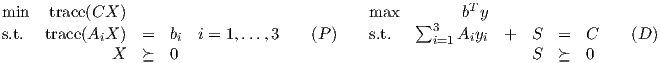
$min trace(CX ) max ∑ bTy s.t. trace(AiX ) = bi i = 1,...,3 (P ) s.t. 3i=1 Aiyi + S = C (D ) X ≽ 0 S ≽ 0$
Show that both (P) and (D) are feasible and both have optimal value equal to zero, but that the optimal value of (P) is not achieved.
Let $[ ] [ ] [ ] [ ] 0 0 1 0 0 1 3 C := 0 9 , A1 := 0 - 1 , A2 := 1 2 , b := 6$
The primal and dual semidefinite programs are
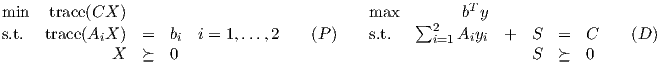
$T min trace(CX ) max ∑2 b y s.t. trace(AiX ) = bi i = 1,...,2 (P ) s.t. i=1 Aiyi + S = C (D ) X ≽ 0 S ≽ 0$
Show that (P) has an optimal value of 9. Is (D) strictly feasible? Show that y = (-1,2) is optimal for (D). Show that the optimal X and S matrices are simultaneously diagonalizable.
1. Formulate the primal problem in Question 4 as an equivalent second order cone program, and solve it using CPLEX. Hint: in AMPL, you should be able to enter a constraint of the following form when x, y, z are variables, with y,z ≥ 0:
  subject to soc: x**2 <= y*z ;
2. Formulate the dual problem in Question 4 as an equivalent second order cone program, and solve it using CPLEX.
1. Construct and solve a second order cone relaxation of the primal SDP in Question 3, by requiring all the principal 1 × 1 and 2 × 2 subdeterminants of X be nonnegative.
2. Construct and solve a second order cone relaxation of the dual SDP in Question 3, by requiring all the principal 1 × 1 and 2 × 2 subdeterminants of S be nonnegative.
Let x ∈ ℝ₊ⁿ. Show that the constraint 1 ≤ Π_i=1ⁿx_i is equivalent to a collection of O(n) second order cone constraints.
Most semidefinite relaxations of combinatorial optimization problems result in a linear constraint on the trace of the primal matrix X. For example, in the relaxation of MaxCut, the diagonal entries are all required to equal one, so the trace must equal the number of nodes. The relaxation of the combinatorial optimization problem gives a primal SDP; assume this primal SDP and its dual are feasible. Show that if the linear constraints of the primal problem imply that any feasible solution must satisfy trace(X) = a for some positive constant a then the feasible region for the dual is unbounded, and strictly feasible dual solutions exist.
The project: Project presentations will be on Wednesday, May 1, from 3-6pm, location Troy 2012. Your presentation should be no more than 15 minutes long. Please bring a device to present your talk with an HDMI port. If this is not possible, let me know in plenty of time. In order to encourage questions, your grade will not be lowered if you are unable to answer questions from other students, but it may be raised. Moreover, I may give some bonus points for asking a particularly good question.
Handouts: Please prepare 12 copies of your slides, to be handed out before your talk.
Reports: Your writeup is due by Tuesday April 30, on LMS. It can go to the same place as this homework. It should describe the problem you worked on, what you did to solve the problem, and the significance of what you did. You should also cite relevant references and state what was novel about your approach. In addition, upload a copy of your slides.
For group projects, each group member should upload a description of his or her individual contribution. (Plain text or pdf is fine.)

John Mitchell	518–276–6915
Amos Eaton 325	mitchj at rpi dot edu
Office hours:	Tues 2.30-4pm, AE 325 (masks required) or webex.
	Thurs 1–2pm, webex: https://rensselaer.webex.com/meet/mitchj