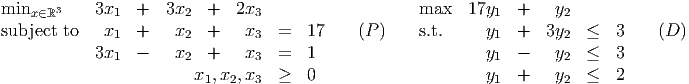
Show that y = (1,-1) is on the central trajectory for this problem. What is the corresponding primal point?
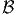 = ∅
= ∅
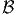 = {1,…,n}.
= {1,…,n}.
Hand in the primal solution for each problem, and discuss whether the three solutions differ for each of the models you chose. If the solutions have too many variables it is fine to select a few variables to display.
The problems are in MPS format at the netlib link. Options for solving them include:
(A) Most of the problems are also available in AMPL format on Box at
https://rpi.box.com/s/5ucl9wog8ey4pcgxnridpehvqc4b74ng
The 00README.txt file explains how to run the AMPL models.
A list of cplex options available in AMPL is available here:
https://dev.ampl.com/solvers/cplex/options.html
Of particular interest are baropt to run an interior point code, crossover to find an optimal BFS after baropt finds a point on the optimal face, and dualopt and primalopt to run different versions of simplex. The commands pgradient and dgradient allow different pricing options within primal simplex and dual simplex, respectively. You can use these options in ampl with the syntax option cplex_options ’...’;
(B) Alternatively, you can run cplex directly, without using ampl, in which case you would read in the MPS file. Standalone versions of cplex can be obtained through the IBM Academic Initiative, by downloading CPLEX Studio.
Useful commands in cplex include read, optimize, and display. You can choose the solver in cplex by issuing the command set lpmethod at the prompt. You can change options in the barrier solver (including the use of crossover) with the command set barrier; unfortunately, crossover seems to no longer give the option of not using it.
(C) My first PhD student, Brian Borchers, has code available to convert MPS files into MATLAB format.