MATP6640/ISYE6770 Linear Programming, Homework 4.

Due: 11.59pm on Friday, March 1, 2022 on LMS.
10% penalty for each day late.

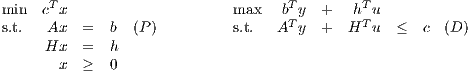
Construct a primal-dual pair of linear programs of the form $min cTx max bTy + hTu s.t. Ax = b (P ) s.t. AT y + HT u ≤ c (D ) Hx = h x ≥ 0$
satisfying all of the following conditions:
- {x ∈ IRⁿ : Hx = h,x ≥ 0} is bounded
- (D) has a unique optimal solution (y^*,u^*)
- A and H each have one row
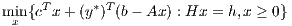
- every optimal basic feasible solution x to the Lagrangian subproblem $T * T mixn{c x+ (y ) (b - Ax) : Hx = h,x ≥ 0}$
  violates Ax = b.
Let
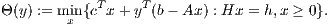
$T T Θ(y) := mixn{c x +y (b - Ax) : Hx = h,x ≥ 0}.$
Is 0 a subgradient of Θ(y^*)?
The directed graph G = (V,E) is as follows:

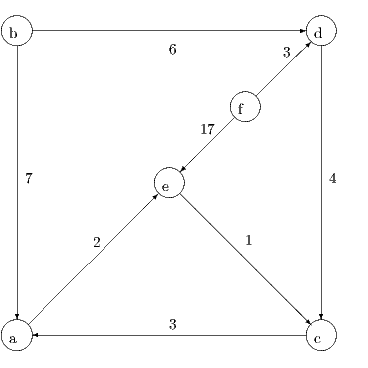
One unit of commodity A must be shipped from b to c and one unit of commodity B must be shipped from f to e. The cost of shipping one unit of flow along an arc is indicated in the figure. The cost is the same for each commodity. Each arc e ∈ E in the graph has capacity equal to one; this is the maximum total flow along the arc for the combination of the two commodities. Used the path-based formulation to find the minimum cost total flow. What is the optimal integral flow?
In a vehicle routing problem, a set of cities {1,…,n} must be visited, starting from a base city 0. More than one vehicle can be used, with each vehicle traversing a subtour that starts and ends at the base but only visits a subset of the cities. There may be constraints on the allowed subtours; for example, no tour can visit more than k cities, or no tour can take longer than U. This problem can be formulated as an integer program with each variable corresponding to an allowable subtour. Let T be the set of allowable subtours. Let c_t be the cost of subtour t ∈ T. Let a^t ∈{0,1}ⁿ be the incidence vector of subtour t ∈ T, so a_i^t = 1 if and only if tour t visits city i for i ∈{1,…,n}. 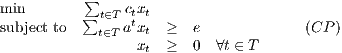The LP relaxation of the vehicle routing problem can then be expressed as $min ∑ cx subject to ∑ t∈Tattxt ≥ e (CP ) t∈T xt ≥ 0 ∀t ∈ T t$
where e denotes the vector of ones. Since the number of possible tours is very large, a column generation approach is used.
Let n = 4. No tour is allowed to visit more than three cities (plus the base city). Assume the cost c_t of a tour is given by the sum of the edge lengths in the tour, and the edge lengths are as follows:

city 0 1 2 3 4
0 – 4 7 9 4
1 4 – 4 6 8
2 7 4 – 7 5
3 9 6 7 – 7
4 4 8 5 7 –

Assume we have 2 initial tours:
$0- 1- 2 - 0 and 0 - 3- 4- 0.$
and an initial primal solution with x_t = 1 for each of the two tours. One optimal dual solution for this set of tours is y = (6,9,13,7)^T. Find at least 4 additional valid tours for which the corresponding dual constraint for (CP) is violated.
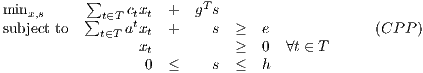
Algorithmically, the problem (CP) in Question 3 is sometimes relaxed to $∑ minx,s ∑ t∈T ctxt + gTs subject to t∈T atxt + s ≥ e (CP P ) xt ≥ 0 ∀t ∈ T 0 ≤ s ≤ h$
where g,h ∈ IRⁿ are nonnegative vectors of parameters. How does this change the dual problem? What benefit do you think this might have?

John Mitchell	518–276–6915
Amos Eaton 325	mitchj at rpi dot edu
Office hours:	Tues 2.30-4pm, AE 325 (masks required) or webex.
	Thurs 1–2pm, webex: https://rensselaer.webex.com/meet/mitchj

city	0	1	2	3	4

0	–	4	7	9	4
1	4	–	4	6	8
2	7	4	–	7	5
3	9	6	7	–	7
4	4	8	5	7	–