Due: 11.59pm on Friday, February 18, 2022 on LMS.
10% penalty for each day late.
Dantzig-Wolfe decomposition solves the linear programming problem
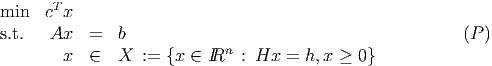
where X is a polyhedron and A is m × n. The procedure solves subproblems of the
form
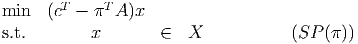
where (π,σ) ∈ IRm+1 is the current dual solution to the Master Problem. Questions 3 and 4
concern Dantzig-Wolfe decomposition.
- Let Q be the polyhedron
![[ ] [ ] [ ] [ ]
Q := {x ∈ IR2 : x = 1 y1 + 2 y2 + 2 z1 + 1 z2,
3 1 1 1
y1 ≥ 0,y2 ≥ 0,z1 ≥ 0,z2 ≥ 0,y1 + y2 = 1}.](hw32x.png)
Use the proof of the affine Weyl theorem (so use Fourier-Motzkin elimination explicitly) to
construct constraints Ax ≥ b such that
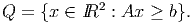
(Note that the y variables correspond to the extreme points and the z variables correspond to
the rays.)
- Suppose we are given the extreme points and extreme rays of a pointed polyhedron
P ⊆ IRn. Let
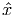 ∈ IRn. Construct a linear programming problem whose solution
provides us with an inequality gT x > gT
∈ IRn. Construct a linear programming problem whose solution
provides us with an inequality gT x > gT 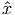 that is satisfied by all x ∈ P and violated
by
that is satisfied by all x ∈ P and violated
by 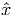 , or allows us to conclude that no such inequality exists. What is the dual of
your LP? Give an interpretation of the dual LP. (Such an inequality defines a
separating hyperplane that separates
, or allows us to conclude that no such inequality exists. What is the dual of
your LP? Give an interpretation of the dual LP. (Such an inequality defines a
separating hyperplane that separates 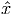 from P. Note that the variables in the LP will
include g.)
from P. Note that the variables in the LP will
include g.)
- When using Dantzig-Wolfe decomposition, assume the current subproblem has an optimal
solution x with value v. Can you give a lower bound on the optimal value of (P)? What does
your lower bound become if the current dual solution (π,σ) to the master problem is dual
feasible?
- Suppose (P) has been solved using Dantzig-Wolfe decomposition. How would you find the
optimal dual solution to the original problem (P)?
- Consider the standard form polyhedron P = {x ∈ IRn : Ax = b,x ≥ 0} where b ∈ IRm
and A ∈ IRm×n of rank m. Prove or give counterexamples to the following two
statements:
- If n = m + 1 then P has at most two basic feasible solutions.
- Consider the problem of minimizing max{cT x,dT x} over P, where c,d ∈ IRn. If
this problem has an optimal solution, it has an optimal solution that is an extreme
point of P.
- The Project:
Along with your solutions to this homework, hand in a brief description of what you
would like to do for the project part of this course. Your project can be one of the
following:
- a topic arising in your research that fits well with the topics covered in the course.
You would work on your own on such a project.
- another project you suggest or I suggest. You can work in groups of up to three
people on such a project. All group members should contribute equally to the
project. Each individual should turn in a one-page description of their contribution
to the project along with the group report.
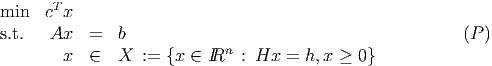
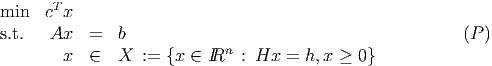
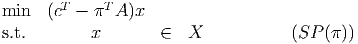
![[ ] [ ] [ ] [ ]
Q := {x ∈ IR2 : x = 1 y1 + 2 y2 + 2 z1 + 1 z2,
3 1 1 1
y1 ≥ 0,y2 ≥ 0,z1 ≥ 0,z2 ≥ 0,y1 + y2 = 1}.](hw32x.png)
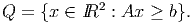
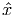 ∈ IRn. Construct a linear programming problem whose solution
provides us with an inequality gT x > gT
∈ IRn. Construct a linear programming problem whose solution
provides us with an inequality gT x > gT 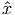 that is satisfied by all x ∈ P and violated
by
that is satisfied by all x ∈ P and violated
by 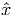 , or allows us to conclude that no such inequality exists. What is the dual of
your LP? Give an interpretation of the dual LP. (Such an inequality defines a
separating hyperplane that separates
, or allows us to conclude that no such inequality exists. What is the dual of
your LP? Give an interpretation of the dual LP. (Such an inequality defines a
separating hyperplane that separates 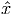 from P. Note that the variables in the LP will
include g.)
from P. Note that the variables in the LP will
include g.)