MATP6640/ISYE6770 Linear Programming, Homework 2.

Due: 11.59pm on Friday, February 2, 2024 on LMS.
10% penalty for each day late.

1.
Assume that both the primal problem minx{cTx : Ax = b,x ≥ 0} and corresponding dual problem maxy,s{bTy : ATy + s = c} are feasible. Here, A is a m × n matrix of rank m, and all vectors are dimensioned appropriately. For each component j = 1,…,n, show that either xj or sj is unbounded in its feasible region, but not both.
2.
Consider the linear programming problem
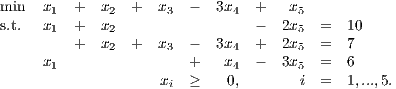
min x1 + x2 + x3 - 3x4 + x5 s.t. x1 + x2 - 2x5 = 10 + x2 + x3 - 3x4 + 2x5 = 7 x1 + x4 - 3x5 = 6 xi ≥ 0, i = 1,...,5.

Let A denote the constraint matrix, and let the basis matrix B consist of columns 2, 3, and 4 of A.

(a)
Find a lower triangular matrix L and an upper triangular matrix U satisfying LB = U.
(b)
Use the factors L and U to calculate xB = B-1b, and hence show we have a basic feasible solution. What is the BFS?
(c)
Use the factors L and U to calculate the reduced cost.
(d)
You should have exactly one negative reduced cost. Use the factors L and U to calculate the corresponding column of B-1N.
(e)
Show that the linear program has an unbounded optimal value. What is the corresponding ray r?
3.
The dual to the linear program in Question 2 is infeasible. Taking nonnegative linear combinations of the dual constraints gives further valid dual constraints. Show how the ray r found in Question 2 can be used to construct a linear combination of the dual constraints that is clearly infeasible.
4.
Use Fourier-Motzkin elimination to show the dual to the problem in Question 2 is infeasible.
5.
Use AMPL or another linear programming package to solve the standard form linear programming problem
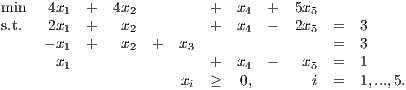
min 4x1 + 4x2 + x4 + 5x5 s.t. 2x1 + x2 + x4 - 2x5 = 3 - x1 + x2 + x3 = 3 x1 + x4 - x5 = 1 xi ≥ 0, i = 1,...,5.

(See the course webpage for more information on AMPL. The software is available on LMS.)

    John Mitchell 518–276–6915
    Amos Eaton 325 mitchj at rpi dot edu
    Office hours: Tues 2.30-4pm, AE 325 (masks required) or webex.
    Thurs 1–2pm, webex: https://rensselaer.webex.com/meet/mitchj