Due: 11.59pm on Friday, January 19, 2024 on LMS.
10% penalty for each day late.

Let (P) be the standard form LP, min{c^Tx : Ax = b,x ≥ 0}. In class, we saw that if a problem of the form (P) has a feasible solution then it has a basic feasible solution. Construct a similar proof to show that if (P) has an optimal solution, it has a basic feasible solution that is optimal.
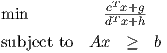
Assume it is known that the fractional linear program $T min cdT-x+xg+h- subject to Ax ≥ b$
has an optimal value in the range [α,β]. In addition, assume that any x satisfying Ax ≥ b also satisfies d^Tx + h > 0. Develop a procedure that uses linear programming as a subroutine to find the optimal value of the fractional linear program, to within any desired tolerance. (Hint: Consider the problem of determining whether the optimal value is above or below a given threshold τ.)
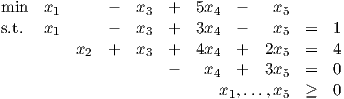
Consider the linear program $min x1 - x3 + 5x4 - x5 s.t. x - x + 3x - x = 1 1 3 4 5 x2 + x3 + 4x4 + 2x5 = 4 - x4 + 3x5 = 0 x1,...,x5 ≥ 0$
The point x = (1,4,0,0,0)^T is a basic feasible solution for this problem. Find all the bases corresponding to this bfs. Use complementary slackness to show that this point is optimal. Find at least 2 optimal dual solutions.
Let A ∈ ℝ^m×n and c ∈ ℝⁿ. Show that exactly one of the following holds:
1. ∃y ∈ ℝ^m s.t. A^Ty = c
2. ∃x ∈ ℝⁿ s.t. Ax = 0,c^Tx≠0.

John Mitchell	518–276–6915
Amos Eaton 325	mitchj at rpi dot edu
Office hours:	Tues 2.30-4pm, AE 325 (masks required) or webex.
	Thurs 1–2pm, webex: https://rensselaer.webex.com/meet/mitchj