Grading policy: 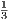 homeworks,
homeworks, 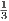 midterm,
midterm, 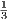 project/presentation. Grades will be posted on LMS.
project/presentation. Grades will be posted on LMS.
MR 12–1:50pm Carnegie 206 Spring 2023
Course Outline
I intend to follow this outline fairly closely, but, if appropriate, I will alter what is included in the course. Problems such as node packing, the traveling salesman problem, the knapsack problem, the quadratic assignment problem, and the MaxCut problem, will be discussed throughout the course.
Lectures: Lecture notes will be posted on LMS.
Homework: Approximately every two weeks. Homework and exam solutions will be made available online. The homeworks will probably contain some computational work. You should learn a fair amount from the homeworks. Therefore, try working out the solutions on your own. If you have difficulties, you may talk to me or to other students about the homeworks, but you must write up your solutions on your own.
Exam: One in-class midterm. As you would expect, the exam must be all your own work. It will take place on or about March 21 (Lecture 18).
Project: The project will involve modeling and computational testing. Depending on the project, the testing may use AMPL or PYOMO or it may use a programming language such as MATLAB or PYTHON or C or FORTRAN. You will write up your solution and give a presentation in class. The presentation will take place either during the last week of classes or during the time scheduled for a final exam. Your project can be one of the following:
Grading policy: 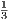 homeworks,
homeworks, 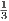 midterm,
midterm, 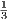 project/presentation. Grades will be posted on LMS.
project/presentation. Grades will be posted on LMS.
Office hours: Tuesday 2–4pm in my office, AE 325.
Thursday 3-4pm on webex, https://rensselaer.webex.com/meet/mitchj
Piazza: This term we will be using Piazza for class discussion. The system is highly catered to getting you help fast and efficiently from classmates and myself. Rather than emailing questions to me, I encourage you to post your questions on Piazza. If you have any problems or feedback for the developers, email team@piazza.com.
Find our class signup link at: https://piazza.com/rpi/spring2023/matp6620
Student learning objectives: Develop a thorough understanding of the theory and algorithms of combinatorial optimization and integer programming. An ability to apply knowledge of mathematics, science and engineering. An ability to design and conduct experiments, as well as to analyze and interpret data. An ability to identify, formulate and solve engineering problems.
Textbooks:
Required:
| |
Conforti, Cornuejols, and Zambelli, Integer Programming. Springer, 2014. More recent than the previous text by Nemhauser and Wolsey (see below). |
|
Recommended: | |
Papadimitriou and Steiglitz, Combinatorial Optimization: Algorithms and Complexity. Prentice Hall 1982. A good alternate text. More graph theory, less polyhedral theory than N&W. Reprinted by Dover in 1998. |
|
Other relevant textbooks: | |
Nemhauser and Wolsey, Integer and Combinatorial Optimization. Wiley, 1988 (paperback 1999). Very detailed, and a standard reference. |
|
Wolsey, Integer Programming. Wiley 1998. Better coverage of heuristics and a little more up-to-date than Nemhauser and Wolsey. |
|
Lee, A First Course in Combinatorial Optimization. Cambridge University Press, 2004. Available online from the library. |
|
Schrijver, Combinatorial Optimization: Polyhedra and Efficiency. Springer Verlag, 2004. Three volumes, encyclopedic. |
|
Garey and Johnson, Computers and Intractability. Freeman, 1979. The bible of NP-completeness. |
|
The World Wide Web: This outline, the homeworks, course notes, and other information will be available via my homepage,
In addition, an RPI LMS page has been set up for this course. The software package AMPL will be available from there.
Academic integrity: Student-teacher relationships are based on mutual trust. Acts which violate this trust undermine the educational process. The Rensselaer Handbook defines various forms of academic dishonesty and procedures for responding to them. The penalties for cheating can include failure in the course, as well as harsher punishments.
You may be able to find solutions to some of the homework problems online. Do not use these solutions.
Appealing grades: As with any other administrative question regarding this course, see me in the first instance. If we are unable to reach agreement, you may appeal my decision to the Head of the Math Sciences department.