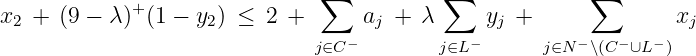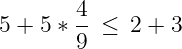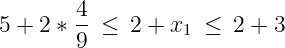Please do all four problems. Show all work. No books or calculators allowed. You may use any result from class, the homeworks, or the texts, except where stated. You may use one sheet of handwritten notes. The exam lasts 110 minutes.

1. (30 points) We consider a fixed charge network flow problem where there are both incoming and outgoing arcs at a node D, as illustrated below.

   

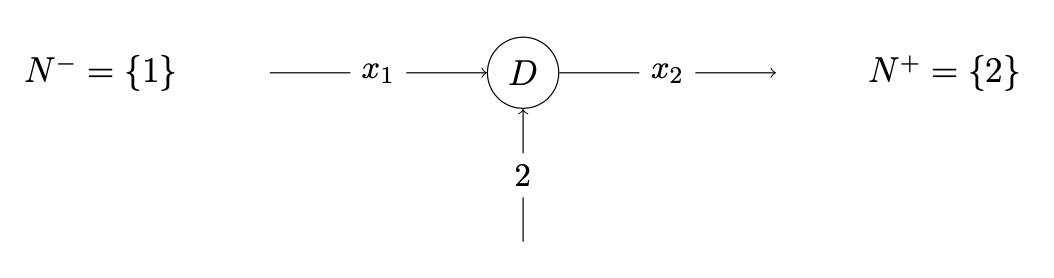
   The flow variables satisfy the fixed charge constraints 0 ≤ x₁ ≤ 3y₁ and 0 ≤ x₂ ≤ 9y₂ where y_j is a binary variable. The set of feasible solutions at D is given by

   

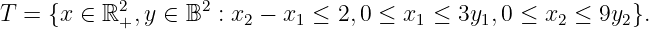
   A fixed charge inequality is

   (1)

   where C^- ⊆ N^- = {1} and L^- ⊆ N^-\ C^- are disjoint subsets and a ₁ = 3 denotes the capacity of the incoming arc. The parameter λ = 9 -∑ _j∈C^-a_j - 2.

   Note: We have three choices for C^- and L^-: (i) C^- = {1},L^- = ∅,N^-\ (C^-∪ L^-) = ∅, (ii) C^- = ∅,L^- = {1},N^-\ (C^-∪ L^-) = ∅, (iii) C^- = ∅,L^- = ∅,N^-\ (C^-∪ L^-) = {1}.

   1. (10 points) Show equation (1) is satisfied by all points in T when y₂ = 1, regardless of the choice of C^- and L^-.

      Solution: We consider the three cases: In each case, the left hand side of (1) becomes x₂ when y₂ = 1

      • C^- = {1}: Here, the right hand side of (1) is 2 + a ₁ = 5 ≥ 2 + x₁. So (1) is weaker than x₂ - x₁ ≤ 2.

      • L^- = {1}: Here, λ = 7. Two subcases: (α) y ₁ = 0: Then x₁ = 0 so from the definition of T we need x₂ ≤ 2, which is equivalent to (1) in this case. (β) y₁ = 1: then (1) becomes x₂ ≤ 2 + 7 = 9, which is weaker than defined in T.

      • N^- \ (C^- ∪ L^-) = {1}: In this case, (1) becomes x ₂ ≤ 2 + x₁, as in the definition of T.

      Hence (1) is satisfied by all points in T with y₂ = 1.

   2. (15 points) Show equation (1) is satisfied by all points in T when y₂ = 0, regardless of the choice of C^- and L^-.

      Solution: Note that y₂ = 0 implies x₂ = 0, so the left hand side of (1) is (9 - λ)⁺. We consider the three cases:

      • C^- = {1}: Here, λ = 4 so the left hand side of (1) is 5. The right hand side of (1) is 2 + a₁ = 5 also, so (1) is satisfied..

      • L^- = {1}: Here, λ = 7 so the left hand side of (1) is 2. The right hand side of (1) is 2 + λy₂ ≥ 2, so the equation is satisfied.

      • N^-\ (C^-∪ L^-) = {1}: In this case, λ = 7 so the left hand side of (1) is 2, and as in the previous case, the right hand side is at least as large.

      Hence (1) is satisfied by all points in T with y₂ = 0.

   3. (5 points) The point x = (3, 5), y = (1,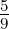) is in the LP relaxation of the feasible region. Show equation (1) is violated by this point, for two different choices of C^- and L^-.

      Solution: Two cases:

      • C^- = {1},L^- = ∅: Here, λ = 4 so (1) becomes

        

        which is clearly violated.

      • C^- = ∅,L^- = ∅: Here, λ = 7 so (1) becomes

        

        which is clearly violated.

2. Let

   

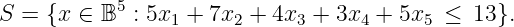
   1. (10 points) Show the valid inequality x₂ + x₄ + x₅ ≤ 2 has Chvatal-Gomory rank equal to one.

      Solution: We take the following nonnegative combination of the original constraints: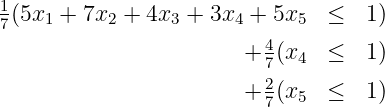

      

      giving the valid inequality

      

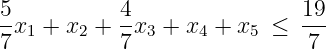
      Rounding down the left hand side then rounding down the right hand side gives the valid inequality x₂ + x₄ + x₅ ≤ 2, showing the inequality does indeed have C-G rank equal to 2.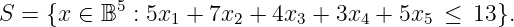

      

   2. (10 points) Show that x₂ + x₄ + x₅ ≤ 2 defines a facet of conv(S).

      Solution: Note first that the knapsack polytope is full-dimensional.

      There are at least 2 methods to show the inequality defines a facet: using lifting, or finding 5 affinely independent feasible solutions on the face. We use the second approach.

      The five points are:

      

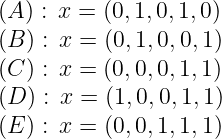
      We show these 5 vectors are linearly independent, placing them as columns of a matrix after permuting the components:

      

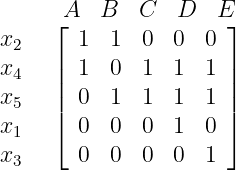
      Subtracting the x₂ row from the x₄ row, and then adding the x₄ row to the x₅ row gives an upper-triangular matrix with nonzeroes on the diagonal. Hence the 5 vectors are linearly independent, so they are affinely independent, so the constraint defines a facet of S.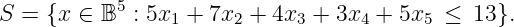

      

   3. (10 points) Strengthen the valid inequality x₁ + x₂ + x₅ ≤ 2 by lifting it.

      Solution: Lifting first on x₃: We solve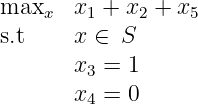

      

      Optimal value is ζ = 11 so lifting coefficient for x₃ is α = 2 - ζ = 1.

      Now lifting on x₄: We solve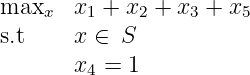

      

      Optimal value is ζ = 2 so lifting coefficient for x₄ is α = 2 - ζ = 0.

      Hence we obtain a lifted inequality of x₁ + x₂ + x₃ + x₅ ≤ 2.

      Note that even if we lift in the opposite order, we obtain the same inequality.

3. Consider the MaxCut problem on K₅, the complete graph on 5 vertices. Let V and E denote the sets of vertices and edges of K₅, respectively. You may assume the convex hull of feasible solutions is full-dimensional.

   1. (5 points) Show from first principles that the maximum number of edges in any cut is 6.

      Solution:

      If all 5 vertices are on the same side of the cut then 0 edges are in the cut.

      If 4 vertices are on 1 side and the last vertex on the other side, then the cut contains 4 edges. If 3 vertices are on 1 side and 2 on the other, then 6 edges are in the cut.

   2. (10 points) It follows from part 3a that the constraint ∑ _e∈Ex_e ≤ 6 is valid for the MaxCut problem on K₅. How would you try to show that this constraint gives a facet of the convex hull of cuts? (Note: I do not want you to show that it is a facet; instead, I want you to tell me what points you might consider, and what you might try to do with those points.)

      Solution:

      It was proved in class that the convex hull of the MaxCut polytope is full-dimensional. K₅ has 10 edges, so the dimension of the convex hull is 10.

      Thus, to prove our inequality is a facet, we need to find 10 affinely independent points that satisfy the constraint at equality.

      There are 10 ways to put three vertices on one side of the cut and 2 on the other, so the incidence vectors of these cuts give the candidate points.

4. (25 points; each part is worth 5 points) For each of the following statements, determine whether it is TRUE or FALSE, and give a short justification (one or two sentences).

   1. If G = (V,E) is a perfect graph then its complement graph is also perfect.

      Solution:

      TRUE: This is a result from the notes.

   2. Let G = (V,E) be a graph. If the maximum cardinality node packing on G has the same size as the minimum cardinality clique cover on G then G is a perfect graph.

      Solution:

      FALSE: need the equality to also hold for every subgraph of G.

   3. The node-arc incidence matrix of an undirected graph is totally unimodular.

      Solution:

      FALSE: It’s true for bipartite graphs and for directed graphs. It’s not true for odd cycles; eg, the 3-cycle gives a node-arc incidence matrix of determinant 2 or -2 (the sign depends on the ordering of the columns).

   4. Assume x ∈ ℝ₊ⁿ satisfies the inequalities g^T x ≥ 1 and h^T x ≥ 1. Then x also satisfies ∑ _j=1ⁿ max{g _j,h_j}x_j ≥ 1.

      Solution:

      TRUE: This is a result from the notes.

   5. Assume the nonnegative integer vector x satisfies x₁ + 0.7x₂ + 0.2x₃ = 5.4. Then x also satisfies 0.2x₂ + 0.2x₃ ≥ 0.4.

      Solution:

      TRUE: this is the strong Gomory cut from the original constraint.

      Alternatively, the constraint is equivalent for x₂ + x₃ ≥ 2. If we look at the three nonnegative integers choices of x₁ and x₂ that violate this constraint, it is easy to see that none of them lead to an integer solution to the original equation.