Name:

MATP6620/ISYE6770
Integer and Combinatorial Optimization
Spring 2021

Midterm Exam, Thursday, April 1, 2021.
Solutions

Please do all six problems. Show all work. You can use your notes and the text books and other material linked from the course webpage, on Box, or LMS, or Piazza. You cannot use online resources such as chegg or google searches, or software such as AMPL or OPL or matlab or desmos. You cannot consult with other students. You may use any result from class, the homeworks, or the texts, except where stated. The exam lasts 150 minutes.

You do not need to print out and fill in this exam, you can write up your solutions separately and scan them in. Please write neatly, since there is almost always a loss in picture quality when scanning!

Make sure you state the last digit of your RIN in the questions that require it.

Q1		/0

Q2		/15

Q3		/15

Q4		/20

Q5		/20

Q6		/30


Total		/100

(0 points) Write out the following honor pledge and sign your name:

I have neither given nor received any illegal aid on this exam.
If the last digit of your RIN is 0,3,7, let a = 3.5. If the last digit of your RIN is 1,4,8, let a = 4.5. If the last digit of your RIN is 2,5,6,9, let a = 5.5.
1. (5 points) Let x ≥ 0 be a continuous variable and let y ≥ 0 be an integer variable. Give the convex hull of
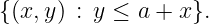
  ${(x,y) : y ≤ a + x}.$
2. (10 points) Use part (a) to give a valid constraint for the following set:
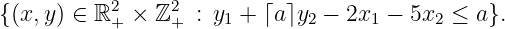
  ${(x, y) ∈ ℝ2+ × ℤ2+ : y1 + ⌈a⌉y2 - 2x1 - 5x2 ≤ a}.$
Solution:
1. Convex hull is all x,y satisfying
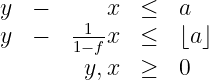
  $y - x ≤ a y - 1-1fx ≤ ⌊a⌋ y,x ≥ 0$
2. We have y = y₁ + ⌈a⌉y₂, x = 2x₁ + 5x₂. Since f = 0.5, the cut is
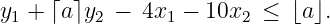
  $y1 + ⌈a⌉y2 - 4x1 - 10x2 ≤ ⌊a⌋.$
  
  Notes:
  - This is the round-down version of the Gomory mixed integer cut.
  - We can’t use the fractional form of the Gomory mixed integer cut, because we don’t have equality with y = a + x.
Consider the matrices
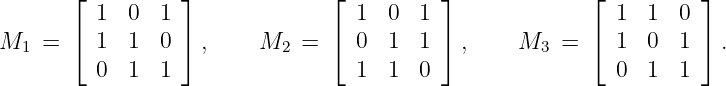
$⌊ 1 0 1 ⌋ ⌊ 1 0 1 ⌋ ⌊ 1 1 0 ⌋ ⌈ ⌉ ⌈ ⌉ ⌈ ⌉ M1 = 1 1 0 , M2 = 0 1 1 , M3 = 1 0 1 . 0 1 1 1 1 0 0 1 1$

If the last digit of your RIN is 0,1,2, let M = M₁. If the last digit of your RIN is 3,4,5,6, let M = M₂. If the last digit of your RIN is 7,8,9, let M = M₃.
1. (5 points) Show M is not totally unimodular.
2. (10 points) Find a subset S of the entries of M with the property that the matrix can be turned into a totally unimodular matrix by changing the sign of the entries in S.
Solution:
1. We have det(M) = ±2, with the sign depending on the particular M.
2. Almost any sign change will work. Eg, if we introduce exactly one -1 in each column then we have an incidence matrix for a directed graph.
(20 points) All the objective function coefficients c_j in the following feasible integer program are integral:
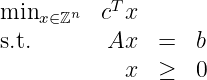
$n T minx∈ℤ c x s.t. Ax = b x ≥ 0$
where A is m × n and all vectors are dimensioned appropriately. The dual to the LP relaxation to this problem can be written
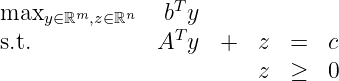
$maxy ∈ℝm,z∈ℝn bTy s.t. AT y + z = c z ≥ 0$
Assume (y,z) is a feasible solution to the dual, with b^Ty non-integral. Let f₀ > 0 denote the fractional part of b^Ty and let f_i denote the fractional part of z_i for i = 1,…,n. Show that any feasible integer solution must satisfy
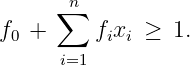
$∑n f0 + fixi ≥ 1. i=1$
(Hint: consider c^Tx.)
Solution:
From dual feasibility, we have
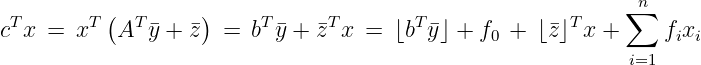
$( ) ∑n cTx = xT AT ¯y + ¯z = bT¯y + ¯zT x = ⌊bT¯y⌋ + f0 + ⌊z¯⌋Tx + fixi i=1$
Now, c^Tx -⌊b^Ty⌋ is integral and strictly greater than ⌊z⌋^Tx ≥ 0. Hence f₀ + ∑ _i=1ⁿf_ix is integral and at least equal to one, so the desired result follows.
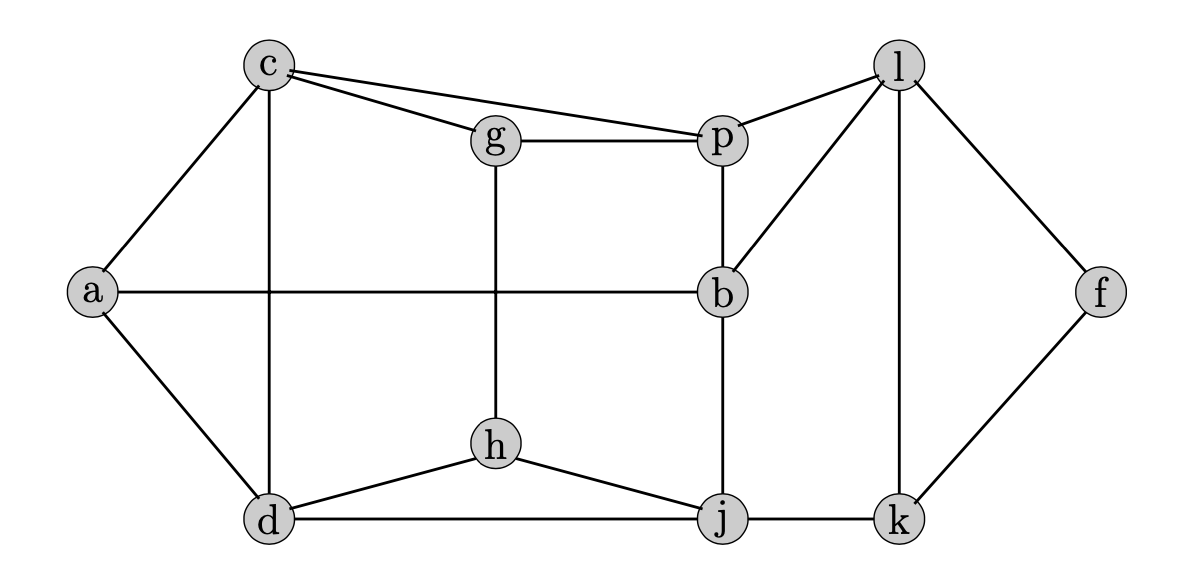
(20 points) If the last digit of your RIN is even, let S = {c,j,l}. If the last digit of your RIN is odd, let S = {d,k,p}.
1. (5 points) Show that the set S is a maximal node packing in this graph.
2. (5 points) The clique polytope is the convex hull of all incidence vectors x ∈ B¹¹ of cliques on this graph. Show the clique polytope has dimension 11.
3. (10 points) Show that the inequality ∑ _i∈Sx_i ≤ 1 defines a facet of the clique polytope.
Solution:
1. It is clear that every other node is adjacent to at least one node in S, so the set S is a maximal node packing.
2. Any vertex on its own is a clique. The empty set is a clique. These 12 incidence vectors are affinely independent, so the set is fill-dimensional.
3. We just consider the case where S = {c,j,l}, the other case is similar.
  11 cliques that satisfy the constraint at equality are:
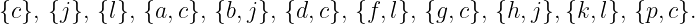
  ${c}, {j}, {l}, {a,c}, {b,j}, {d, c}, {f, l}, {g,c}, {h,j},{k, l}, {p,c}.$
  The incidence vectors of these 11 cliques are linearly independent, so they are affinely independent, so the inequality defines a face of dimension at least 10. Since the set is full-dimensional and the inequality is nontrivial, this is sufficient to argue that we have a facet.
  Alternatively, could prove this using lifting:
  First, argue that when we are in 3-space, with only variables x_c, x_j, x_l, we do have a facet. (Exercise.)
  Then as we lift to include each other vertex i, we get the subproblem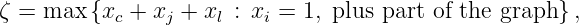
  $ζ = max {x + x + x : x = 1, plus part of the graph} , c j l i$
  which has optimal value 1. So lifting coefficient for x_i is π_i = 1 - 1 = 0. (Should show this more carefully for full credit.)
  So overall lifted constraint is the given constraint.
(30 points) Define the four polyhedra in ℝ³:
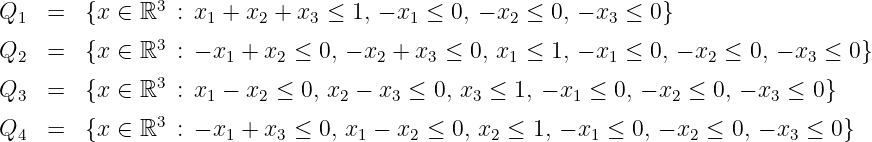
$Q1 = {x ∈ ℝ3 : x1 + x2 + x3 ≤ 1, - x1 ≤ 0, - x2 ≤ 0, - x3 ≤ 0} Q2 = {x ∈ ℝ3 : - x1 + x2 ≤ 0, - x2 + x3 ≤ 0, x1 ≤ 1, - x1 ≤ 0, - x2 ≤ 0, - x3 ≤ 0} 3 Q3 = {x ∈ ℝ : x1 - x2 ≤ 0, x2 - x3 ≤ 0, x3 ≤ 1, - x1 ≤ 0, - x2 ≤ 0, - x3 ≤ 0} Q4 = {x ∈ ℝ3 : - x1 + x3 ≤ 0, x1 - x2 ≤ 0, x2 ≤ 1, - x1 ≤ 0, - x2 ≤ 0, - x3 ≤ 0}$

If the last digit of your RIN is 0,2,5,9, let P = Q₁ ∪ Q₂ and x = (1, 0, 1). If the last digit of your RIN is 1,6,8, let P = Q₁ ∪Q₃ and x = (1, 0, 1). If the last digit of your RIN is 3,4,7, let P = Q₁ ∪ Q₄ and x = (0, 1, 1).
1. (10 points) Set up the cut generation linear programming problem to find valid inequalities for P that are violated by x.
2. (10 points) If the last digit of your RIN is 0,2,5,9, show that x₁ - x₂ + x₃ ≤ 1 is valid for Q₁ and Q₂.
  If the last digit of your RIN is 1,6,8, show that x₁ - x₂ + x₃ ≤ 1 is valid for Q₁ and Q₃.
  If the last digit of your RIN is 3,4,7, show that -x₁ + x₂ + x₃ ≤ 1 is valid for Q₁ and Q₄.
3. (10 points) Show that the inequality in part (b) corresponds to a feasible solution to your LP in part (a).
Solution:
1. We are in the setting in the notes, so:
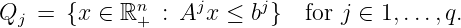
  $n j j Qj = {x ∈ ℝ + : A x ≤ b} for j ∈ 1,...,q.$
  
  Our feasible region is the union of polyhedra. The general form of the cut generation LP to find a valid cut π^Tx ≤ π₀: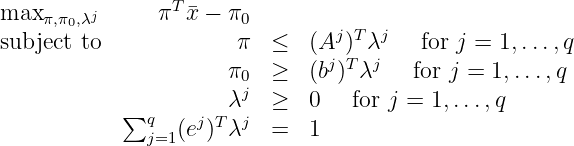
  $max j πT ¯x - π0 π,π0,λ j T j subject to π ≤ (Aj)T λj for j = 1,...,q π0 ≥ (b) λ for j = 1,...,q ∑ λj ≥ 0 for j = 1,...,q qj=1(ej)Tλj = 1$
  
  The three cases:
  - P = Q₁ ∪ Q₂: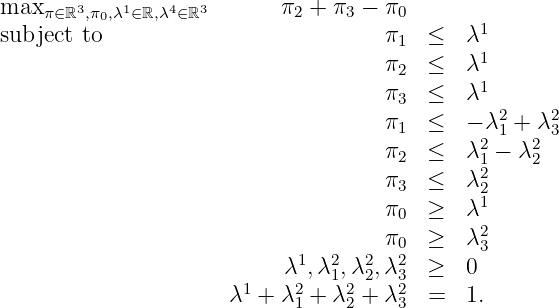
    $max π∈ℝ3,π0,λ1∈ℝ,λ4∈ℝ3 π2 + π3 - π0 subject to π1 ≤ λ1 π2 ≤ λ1 1 π3 ≤ λ 2 2 π1 ≤ - λ1 + λ3 π2 ≤ λ21 - λ22 π3 ≤ λ22 π0 ≥ λ1 2 1 2 2 π02 ≥ λ 3 λ ,λ1,λ 2,λ3 ≥ 0 λ1 + λ21 + λ22 + λ23 = 1.$
  - P = Q₁ ∪ Q₃: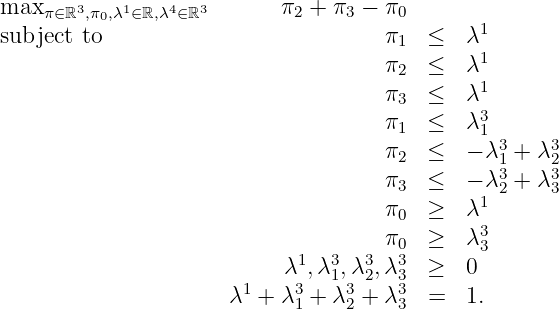
    $max π∈ℝ3,π0,λ1∈ℝ,λ4∈ℝ3 π2 + π3 - π0 subject to π1 ≤ λ1 π ≤ λ1 2 1 π3 ≤ λ 3 π1 ≤ λ 1 π2 ≤ - λ31 + λ32 π3 ≤ - λ3 + λ3 π ≥ λ1 2 3 0 3 π0 ≥ λ 3 λ1,λ31,λ32,λ33 ≥ 0 λ1 + λ31 + λ32 + λ33 = 1.$
  - P = Q₁ ∪ Q₄: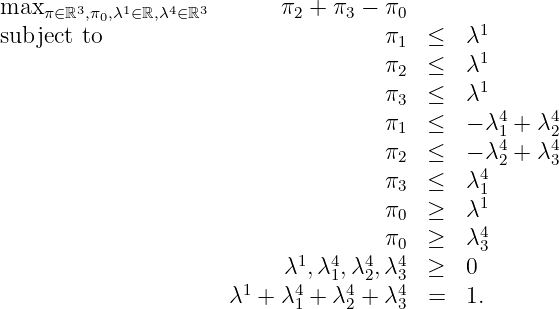
    $max π∈ℝ3,π0,λ1∈ℝ,λ4∈ℝ3 π2 + π3 - π0 subject to π1 ≤ λ1 π2 ≤ λ1 π3 ≤ λ1 4 4 π1 ≤ - λ14 + λ24 π2 ≤ - λ2 + λ3 π3 ≤ λ41 π0 ≥ λ1 π0 ≥ λ4 1 4 4 4 3 1 λ4,λ1,λ4 2,λ34 ≥ 0 λ + λ1 + λ2 + λ3 = 1.$
2. Three cases:
  - P = Q₁ ∪ Q₂:
    Note that the given inequality is valid for P since: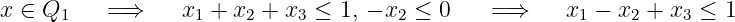
    $x ∈ Q1 =⇒ x1 + x2 + x3 ≤ 1, - x2 ≤ 0 = ⇒ x1 - x2 + x3 ≤ 1$
    and
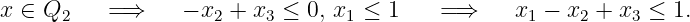
    $x ∈ Q2 =⇒ - x2 + x3 ≤ 0, x1 ≤ 1 =⇒ x1 - x2 + x3 ≤ 1.$
  - P = Q₁ ∪ Q₃:
    Note that the given inequality is valid for P since: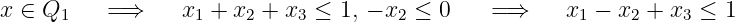
    $x ∈ Q1 =⇒ x1 + x2 + x3 ≤ 1, - x2 ≤ 0 = ⇒ x1 - x2 + x3 ≤ 1$
    and
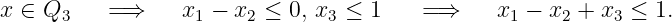
    $x ∈ Q =⇒ x - x ≤ 0, x ≤ 1 =⇒ x - x + x ≤ 1. 3 1 2 3 1 2 3$
  - P = Q₁ ∪ Q₄:
    Note that the given inequality is valid for P since: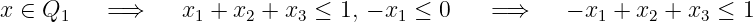
    $x ∈ Q1 =⇒ x1 + x2 + x3 ≤ 1, - x1 ≤ 0 =⇒ - x1 + x2 + x3 ≤ 1$
    and
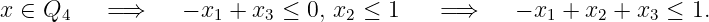
    $x ∈ Q4 =⇒ - x1 + x3 ≤ 0, x2 ≤ 1 =⇒ - x1 + x2 + x3 ≤ 1.$
3. Three cases:
  - P = Q₁ ∪ Q₂: We rescale the inequality so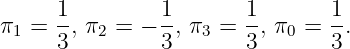
    $π1 = 1-, π2 = - 1, π3 = 1-, π0 = 1-. 3 3 3 3$
    This gives a positive objective function value in the CGLP, and it is feasible with
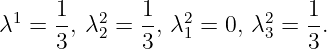
    $1 1 1 λ1 = --, λ22 =--, λ21 = 0, λ23 =-. 3 3 3$
  - P = Q₁ ∪ Q₃: We rescale the inequality so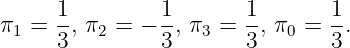
    $1- 1- 1- 1- π1 = 3 , π2 = - 3, π3 = 3 , π0 = 3 .$
    This gives a positive objective function value in the CGLP, and it is feasible with
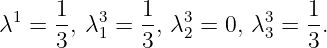
    $1 1- 3 1- 3 3 1- λ = 3 , λ1 = 3 , λ 2 = 0, λ3 = 3 .$
  - P = Q₁ ∪ Q₄: We rescale the inequality so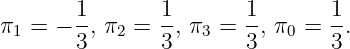
    $1 1 1 1 π1 = - -, π2 = -, π3 = --, π0 =--. 3 3 3 3$
    This gives a positive objective function value in the CGLP, and it is feasible with
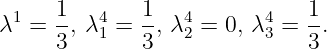
    $λ1 = 1-, λ4 = 1-, λ4 = 0, λ4 = 1-. 3 1 3 2 3 3$