Name:

MATP6620/ISYE6770
Integer and Combinatorial Optimization
Spring 2021

Midterm Exam, Thursday, April 1, 2021.

Please do all six problems. Show all work. You can use your notes and the text books and other material linked from the course webpage, on Box, or LMS, or Piazza. You cannot use online resources such as chegg or google searches, or software such as AMPL or OPL or matlab or desmos. You cannot consult with other students. You may use any result from class, the homeworks, or the texts, except where stated. The exam lasts 150 minutes.

You do not need to print out and fill in this exam, you can write up your solutions separately and scan them in. Please write neatly, since there is almost always a loss in picture quality when scanning!

Make sure you state the last digit of your RIN in the questions that require it.

Q1       /0
Q2       /15
Q3       /15
Q4       /20
Q5       /20
Q6       /30
Total      /100
  1. (0 points) Write out the following honor pledge and sign your name:

    I have neither given nor received any illegal aid on this exam.

  2. If the last digit of your RIN is 0,3,7, let a = 3.5. If the last digit of your RIN is 1,4,8, let a = 4.5. If the last digit of your RIN is 2,5,6,9, let a = 5.5.
    1. (5 points) Let x ≥ 0 be a continuous variable and let y ≥ 0 be an integer variable. Give the convex hull of
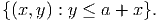
      { (x, y) : y ≤ a + x}.

    2. (10 points) Use part (a) to give a valid constraint for the following set:
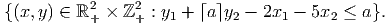
      {(x, y) ∈ ℝ2 × ℤ2 : y + ⌈a⌉y - 2x - 5x ≤ a}. + + 1 2 1 2

  3. Consider the matrices
    ⌊ ⌋ ⌊ ⌋ ⌊ ⌋ 1 0 1 1 0 1 1 1 0 M = ⌈ 1 1 0 ⌉ , M = ⌈ 0 1 1 ⌉ , M = ⌈ 1 0 1 ⌉ . 1 2 3 0 1 1 1 1 0 0 1 1

    If the last digit of your RIN is 0,1,2, let M = M1. If the last digit of your RIN is 3,4,5,6, let M = M2. If the last digit of your RIN is 7,8,9, let M = M3.

    1. (5 points) Show M is not totally unimodular.
    2. (10 points) Find a subset S of the entries of M with the property that the matrix can be turned into a totally unimodular matrix by changing the sign of the entries in S.
  4. (20 points) All the objective function coefficients cj in the following feasible integer program are integral:
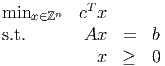
    min n cTx x∈ℤ s.t. Ax = b x ≥ 0

    where A is m × n and all vectors are dimensioned appropriately. The dual to the LP relaxation to this problem can be written

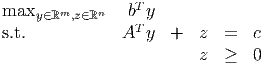
    maxy ∈ℝm,z∈ℝn bTy s.t. AT y + z = c z ≥ 0

    Assume (y,z) is a feasible solution to the dual, with bT y non-integral. Let f 0 > 0 denote the fractional part of bT y and let f i denote the fractional part of zi for i = 1,…,n. Show that any feasible integer solution must satisfy

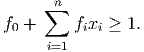
    ∑n f0 + fixi ≥ 1. i=1

    (Hint: consider cT x.)

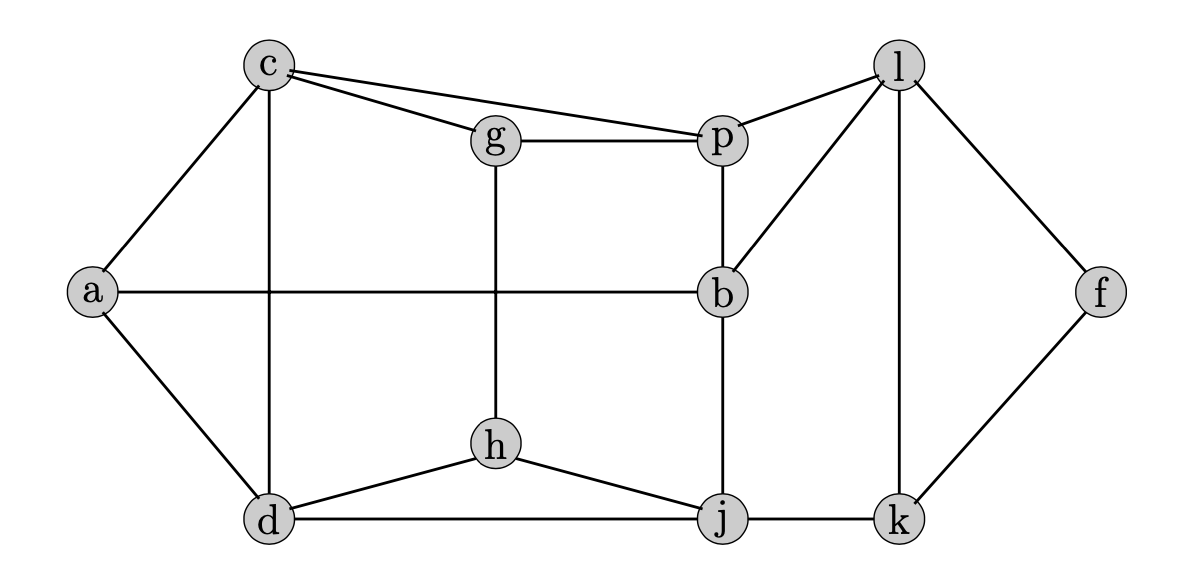
  5. (20 points) If the last digit of your RIN is even, let S = {c,j,l}. If the last digit of your RIN is odd, let S = {d,k,p}.

    1. (5 points) Show that the set S is a maximal node packing in this graph.
    2. (5 points) The clique polytope is the convex hull of all incidence vectors x ∈ B11 of cliques on this graph. Show the clique polytope has dimension 11.
    3. (10 points) Show that the inequality ∑ i∈Sxi ≤ 1 defines a facet of the clique polytope.
  6. (30 points) Define the four polyhedra in ℝ3:
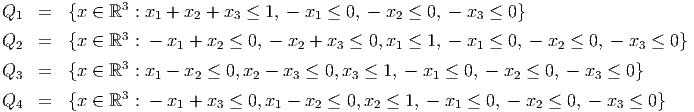
    Q1 = {x ∈ ℝ3 : x1 + x2 + x3 ≤ 1, - x1 ≤ 0, - x2 ≤ 0, - x3 ≤ 0} Q2 = {x ∈ ℝ3 : - x1 + x2 ≤ 0, - x2 + x3 ≤ 0,x1 ≤ 1, - x1 ≤ 0, - x2 ≤ 0, - x3 ≤ 0} 3 Q3 = {x ∈ ℝ : x1 - x2 ≤ 0,x2 - x3 ≤ 0,x3 ≤ 1, - x1 ≤ 0, - x2 ≤ 0, - x3 ≤ 0 } Q4 = {x ∈ ℝ3 : - x1 + x3 ≤ 0,x1 - x2 ≤ 0, x2 ≤ 1, - x1 ≤ 0, - x2 ≤ 0, - x3 ≤ 0}

    If the last digit of your RIN is 0,2,5,9, let P = Q1 ∪ Q2 and x = (1, 0, 1). If the last digit of your RIN is 1,6,8, let P = Q1 ∪Q3 and x = (1, 0, 1). If the last digit of your RIN is 3,4,7, let P = Q1 ∪ Q4 and x = (0, 1, 1).

    1. (10 points) Set up the cut generation linear programming problem to find valid inequalities for P that are violated by x.
    2. (10 points) If the last digit of your RIN is 0,2,5,9, show that x1 - x2 + x3 ≤ 1 is valid for Q1 and Q2.

      If the last digit of your RIN is 1,6,8, show that x1 - x2 + x3 ≤ 1 is valid for Q1 and Q3.

      If the last digit of your RIN is 3,4,7, show that -x1 + x2 + x3 ≤ 1 is valid for Q1 and Q4.

    3. (10 points) Show that the inequality in part (b) corresponds to a feasible solution to your LP in part (a).