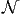
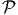 -complete. (No partial credit. 4 points per part, -1 point for incorrect
answers.)
-complete. (No partial credit. 4 points per part, -1 point for incorrect
answers.)
- Node packing with lower bound: Given a graph G = (V,E) and an integer k, does
there exist a node packing of cardinality at least k?
Polynomially solvable
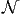
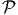 -complete
-complete - Perfect matching: Given a graph G = (V,E), does there exist a perfect matching?
Polynomially solvable
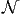
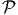 -complete
-complete - Minimum spanning tree with upper bound Given a graph G = (V,E), edge weights we for
e ∈ E, and an integer W, does there exist a spanning tree with total weight no larger
than W?
Polynomially solvable
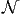
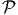 -complete
-complete - Traveling salesman problem with upper bound: Given a complete graph on vertices V ,
with integer edge weights we, and a positive integer W, does there exist a traveling
salesman tour of length no more than W?
Polynomially solvable
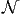
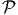 -complete
-complete - Binary knapsack problem with lower bound: Given a ∈ ℤn, c ∈ ℤn, and scalars b and z,
does there exist a binary x ∈ ℤn with aT x ≤ b and cT x ≥ z?
Polynomially solvable
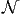
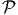 -complete
-complete
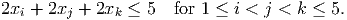
- (4 points) Show the constraints
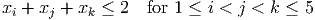
have Chvatal rank equal to one.
- (8 points) Show the valid constraint
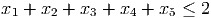
has Chvatal rank no greater than 3.
- (8 points) Show the valid constraint
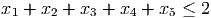
has Chvatal rank at least 2.
Solution:
- We take 0.5 of the original constraint and round down:
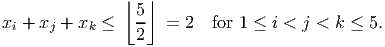
- We use the rank 1 inequality from part (a) to construct the rank 2 inequalities with
sums of 4 variables, and then combine these to give the desired inequality, so it has rank
no greater than 3:
For any 1 ≤ i < j < k < l ≤ 5, we take
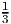 of the four inequaities from part (a) involving
these variables:
of the four inequaities from part (a) involving
these variables:
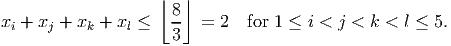
We now take
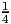 of these 5 inequalities to give
of these 5 inequalities to give
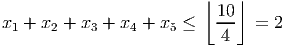
as required.
- The optimal solution to the LP relaxation with objective function max ∑
j=15x
j is
x = (
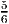 ,
,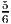 ,
,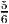 ,
,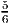 ,
,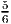 ), with value 4
), with value 4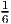 . Since this value is greater than 3, the desired inequality
cannot have Chvatal rank 1.
. Since this value is greater than 3, the desired inequality
cannot have Chvatal rank 1.
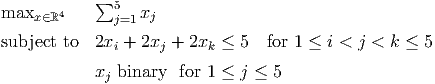
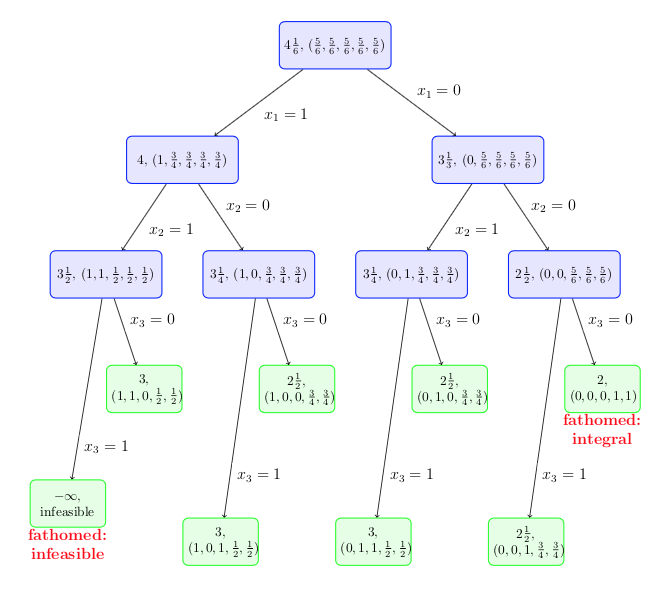
- (10 points) Give the next level of the branch-and-bound tree using standard
branch-and-bound. You need only give the optimal value at each node, together with
the fathoming decision. Note that in an optimal solution to a relaxation, all the
variables that take non binary values take the same value.
- (10 points) Give the tree you obtain if you use orbital branching. How many LP
subproblems do you solve?
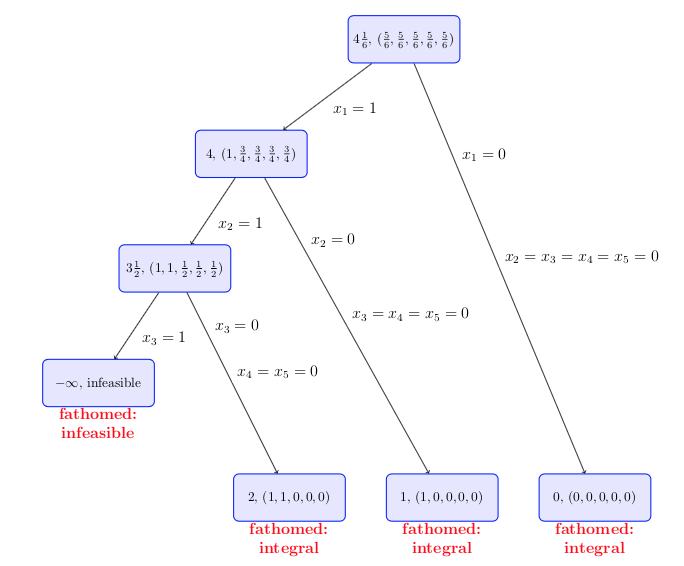
Thus, we need only solve 7 linear programs.
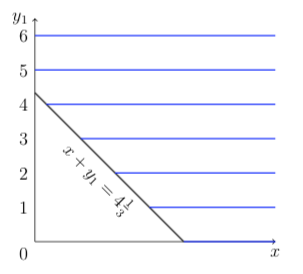
- (8 points) The nonnegative integer variable y1 and the nonnegative continuous variable
x must satisfy
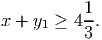
Give a valid linear constraint that is violated by the point x = 0, y = 4
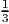 .
.
- (12 points) Let y2 be a binary variable. Assume in addition that y1 and y2 must
satisfy
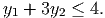
Lift the constraint you found in part 4a to give a valid constraint in x, y1, and y2.
Solution:
- The mixed integer cut is
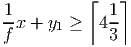
where f =
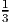 , the fractional part of the right hand side. Can rewrite this
as
, the fractional part of the right hand side. Can rewrite this
as
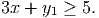
- The lifting subproblem is
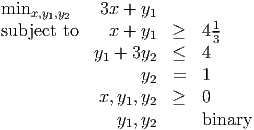
Optimal solution is x = 3
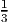 , y1 = 1, y2 = 1, with value 11. Taking the difference between
this value and the right hand side of 5 for the constraint shows that y2 has coefficient -6,
so the lifted constraint is
, y1 = 1, y2 = 1, with value 11. Taking the difference between
this value and the right hand side of 5 for the constraint shows that y2 has coefficient -6,
so the lifted constraint is
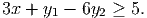
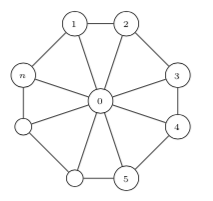
Every feasible solution satisfies the n + 1 degree constraints
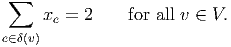
You may assume these equality constraints are linearly independent. (Hint: Let M be a square matrix with every entry equal to one. Let I be the identity matrix. You may assume that the columns of the matrix M - I are linearly independent.)
- (4 points) How many feasible solutions are there?
- (8 points) Show that the dimension of the feasible region is n - 1.
- (8 points) Show that the constraints xe ≤ 1 define facets of conv(S) for the edges (1, 2), (2, 3), …, (n - 1,n), (1,n).
Solution:
- There are n feasible solutions: omit one of the rim edges.
- If we order the n rim edges first, the first n components of the incidence vectors
of our n solutions give the columns of the matrix M - I. Thus, these incidence
vectors are linearly independent, so they are affinely independent. Therefore, the
dimension of the feasible region is at least n - 1.
The region S satisfies n + 1 linearly independent equality constraint, so the dimension of the feasible region is no greater than 2n - (n + 1) = n - 1.
- Just one of the feasible solutions does not satisfy xe = 1 for the listed edges. Hence, we have n-1 feasible solutions that satisfy the constraint at equality. From part (b), these feasible solutions are linearly independent, so they are affinely independent. Thus, the dimension of the face is at least n - 2, so it is a facet.