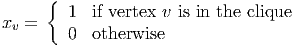
and we denote the set of feasible vectors x by S.
- (10 points) Show that dim(S) = n.
- (10 points) An independent subset U ⊆ V is a collection of vertices, no two of which are
adjacent in G. Any clique contains at most one of the vertices in U. Show that the
corresponding inequality
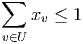
defines a facet of the convex hull of S if U is a maximal independent set.
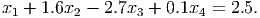 | (1) |
- (7 points) Give a linear inequality of the form g2x2 + g3x3 + g4x4 ≥ 1 that must be satisfied by {x2,x3,x4} if x1 ≤ 2.
- (8 points) Give a linear inequality of the form h2x2 + h3x3 + h4x4 ≥ 1 that must be satisfied by {x2,x3,x4} if x1 ≥ 3.
- (5 points) Argue why the inequality
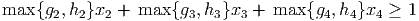
is valid for any nonnegative integer solution to (1). Write down the inequality.
- We can define a new variable y1 so that
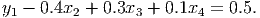
(2)
 :
:
The partition problem: Given n positive integers {a1,…,an} with sum ∑ j=1na j even, does there exist a subset J ⊆{1,…,n} such that
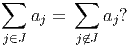
2-machine scheduling: Given two identical machines, m jobs requiring positive integer processing time bj for j = 1,…,m, and a positive integer T, can the jobs be scheduled so that all the jobs are finished by time T? Note that each job must be processed on exactly one machine, each machine can only process one job at a time, once a job is started it must be run to completion, and the jobs can be processed in any order.
- (10 points) Show that any instance of the partition problem can be polynomially transformed into an equivalent instance of the 2-machine scheduling problem.
- (5 points) Assume the 2-machine scheduling problem is
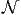
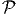 -Complete. Can we
conclude that the partition problem is
-Complete. Can we
conclude that the partition problem is 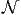
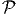 -Complete?
-Complete?
- (5 points) Assume the partition problem is
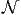
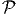 -Complete. Can we conclude that
the 2-machine scheduling problem is
-Complete. Can we conclude that
the 2-machine scheduling problem is 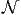
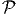 -Complete?
-Complete?
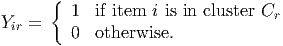
Let eq represent the q-dimensional vector of ones.
- (10 points) Show that Y ek = en and Y T en = pek.
- To set up a semidefinite programming relaxation of the clustering problem, we can
define an n × n matrix X = Y Y T .
- (10 points) Show each diagonal entry of X is equal to one.
- (5 points) What is the value of the product Xen?