Name:

MATP6620/ISYE6770
Combinatorial Optimization and Integer Programming
Spring 2013

Midterm Exam, Friday, April 19, 2013.

Please do all four problems. Show all work. No books or calculators allowed. You may use any result from class, the homeworks, or the texts, except where stated. You may use one sheet of handwritten notes. The exam lasts 110 minutes.

  1. (30 points; each part is worth 10 points)
    1. The binary variables x1, x2, x3, x4, and x5 must satisfy the knapsack constraint
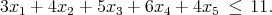
      3x1 + 4x2 + 5x3 + 6x4 + 4x5 ≤ 11.
      		(1)

      Show that the valid cover inequality

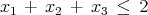
      x1 + x2 + x3 ≤ 2

      has Chvatal rank equal to one. (Note: You will need to use the valid inequalities xi ≤ 1 in your derivation.)

    2. The binary variables xi, i = 1,…,n must satisfy the knapsack constraint
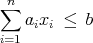
      n∑ aixi ≤ b i=1
      		(2)

      where b and ai, i = 1,…,n are positive scalars. Assume b > ai for i = 1,…,n. Assume further that there exists a subset J ⊆{1,…,n} with

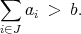
      ∑ ai > b. i∈J
      		(3)

      1. Give a valid cover inequality constraint.
      2. Show that your cover inequality has Chvatal rank equal to one.
  2. (20 points)

    The Node Packing and Max Clique feasibility problems can be described as follows:

    Node Packing: Given a graph G = (V,E) and a integer k, does there exist a subset U ⊆ V with ∣ U∣ ≥ k where no two of the vertices in U share an edge?
    Max Clique: Given a graph G = (V,E) and an integer p, does there exist a clique W ⊆ V with with ∣ W∣ ≥ p?

    Using the fact that Node Packing is NP-Complete, show that the Max Clique problem is NP-complete.

  3. (30 points; each part is worth 10 points)
    1. Assume the nonnegative scalar integer variable y and the nonnegative scalar continuous variable x satisfy the inequality
      x + y ≥ b
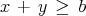
      		(4)

      where b is a non-integral scalar parameter. Let f be the fractional part of b, so b = ⌊b⌋ + f and 0 < f < 1. Prove that the inequality

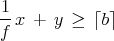
      1-x + y ≥ ⌈b⌉ f
      		(5)

      is valid.

    2. The optimal solution of the LP relaxation of the mixed integer program
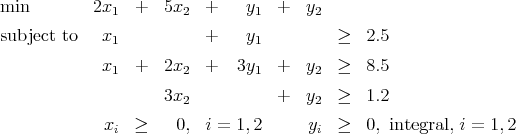
      min 2x1 + 5x2 + y1 + y2 subject to x1 + y1 ≥ 2.5 x1 + 2x2 + 3y1 + y2 ≥ 8.5 3x2 + y2 ≥ 1.2 xi ≥ 0, i = 1, 2 yi ≥ 0, integral, i = 1,2

      is x1 = x2 = 0, y1 = 2.5, y2 = 1.2.

      1. Give three valid inequalities of the type in part 3a that are violated by the solution to the LP relaxation.
      2. Show that none of your inequalities is implied by the other two.
  4. (20 points)

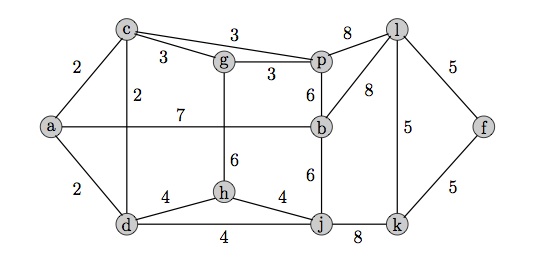
    Show that the shortest Hamiltonian cycle in the following graph has length 50. Make sure to prove your solution is optimal.