67.612/92.672/66.612
Combinatorial Optimization and Integer Programming
Spring 95

Midterm Exam, Monday, April 3, 1995.

Please do all four problems. Show all work. No books or calculators allowed. You may use any result from class, the homeworks, or the texts, except where stated. You may use one sheet of handwritten notes. The exam lasts two hours.

1.

(25 points) Consider a bipartite graph G=(V,E), where V can be broken into two parts U and W, and every edge in E has one endpoint in U and one in W. (Formally, $V=U\cup W$, $U\cap W =\emptyset$, and $e \in E$ implies that e=(i,j), where $i\in U$ and $j\in W$.) Let $k=\mid\!U\!\mid$ and $l=\mid\!W\!\mid$. Note that we have not assumed that every vertex in U is adjacent to every vertex in W. Because this is a bipartite graph, the maximum cardinality matching problem can be solved by solving its linear programming relaxation

$$\begin{array}{lrclrr} \max & \sum_{(i,j) \in E} x_{ij} \\ ... ...j=1,...,l \\ & x_{ij} & \geq & 0, & (i,j) \in E \end{array}$$

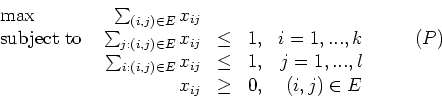
where x_ij is one if edge (i,j) is in the matching, and zero otherwise. Every basic feasible solution to both (P) and its dual (D) is integral.

(a)

(5 points) What is the dual (D) to the linear program (P)? (Hint: The dual of a linear program of the form 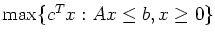$\max\{c^Tx:Ax\leq b,x\geq 0\}$ is $\min\{b^Ty:A^Ty\geq c, y\geq 0\}$.)

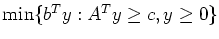(b)

(10 points) A node cover of G is a subset S of V such that every edge in E is incident to at least one vertex in S. What do the integral solutions to (D) correspond to? What do you conclude from strong duality?

(c)

(10 points) What are the complementary slackness conditions for the pair (P) and (D)? Interpret these conditions.

2.

(25 points) An instance of the Hamiltonian Circuit problem is given by:

Given a graph G=(V,E), does there exist a circuit that visits every vertex in V?

We saw in class that the Hamiltonian circuit problem is NP-Complete. An instance of the Hamiltonian Path problem is given by:

Given a graph G=(V,E), does there exist a path that visits every vertex in V?

Use the fact that the Hamiltonian circuit problem is NP-Complete to show that the Hamiltonian path problem is NP-Complete.

3.

(25 points) Consider the node packing problem on the graph G=(V,E). This can be written

$$\begin{array}{lrcll} \max & \sum_{i\in V} x_i \\ \mbox{s... ...\in E \\ & x_i & = & 0 \mbox{ or } 1, & i \in V \end{array}$$

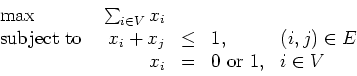
(a)

(10 points) We saw in class that if the vertices v₁,...,v_2k+1 (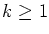$k\geq 1$, k integer) give a circuit then the odd hole inequality

$$\sum_{i=1}^{2k+1} x_i \leq k$$

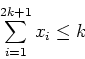
is valid for the node packing polytope. What is the Chvatal rank of this inequality?

(b)

(15 points) We saw in class that if the vertices v₁,...,v_2k+1 (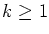$k\geq 1$, k integer) form a clique then the clique inequality

$$\sum_{i=1}^{2k+1} x_i \leq 1$$

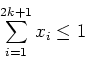
is a facet of the node packing polytope. What is the Chvatal rank of this inequality when k=1? Show that the Chvatal rank of this inequality is no more than 2 if k=2.

4.

(25 points) Let G=(V,E) be a complete graph on m vertices, and let n=m(m-1)/2 be the number of edges. The set of matchings on G is

$$S=\{x\in\Re^n:\sum_{e\in\delta(v)}x_e \leq 1 \mbox{ for } v... ... \mbox{ and } x_e = 0 \mbox{ or } 1 \mbox{ for } e=1,...,n\},$$

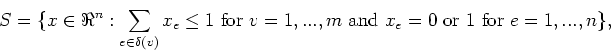
where $\delta(v)$ is the set of vertices adjacent to vertex v.

(a)

(10 points) Show that the dimension of S is n.

(b)

(15 points) An odd set constraint has the form

$$\sum_{e \in E(U)} x_e \leq (\mid\!U\!\mid-1)/2$$

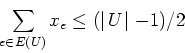
where U is a subset of V of odd cardinality and E(U) is the edges in E that have both endpoints in U. We saw in class that this inequality is valid for S. Show that it is a facet of S when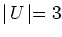 $\mid\!U\!\mid=3$.