Please do all four problems. Show all work. No books or calculators allowed. You may use any result from class, the homeworks, or the texts, except where stated. You may use one sheet of handwritten notes. The exam lasts 110 minutes.

1. (20 points; each part is worth 10 points)
   1. The binary variables x₁, x₂, x₃, and x₄ must satisfy the constraint

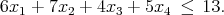
      Find a minimal cover inequality. Lift the cover inequality.

   2. The binary variables z₁, z₂, z₃, and z₄ must satisfy the constraint

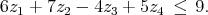
      Use the results of part (a) to derive an inequality that defines a facet of the set of z IB⁴ satisfying the constraint. Why is your constraint facet-defining?

2. (20 points)

   The linearly dependent vectors x¹,…,x^m in IRⁿ are all on the hyperplane a^T x = b, where b≠0. Show that they are affinely dependent.

3. (20 points)

   Let G = (V,E) be a graph with nonnegative edge weights w_e.

   1. (15 points) Show that the problem of finding the maximum weight matching on G is equivalent to finding a maximum weight perfect matching on another graph G′ = (V ′,E′) with nonnegative edge weights w_e′, where V ′ and E′ are obtained from V and E by adding certain vertices and edges.
   2. (5 points) Given a maximum weight perfect matching problem, how can you construct an equivalent minimum weight perfect matching problem with nonnegative edge weights?
4. (40 points; 6 parts on 3 pages)

   This question is concerned with node packings in the following graph.

   
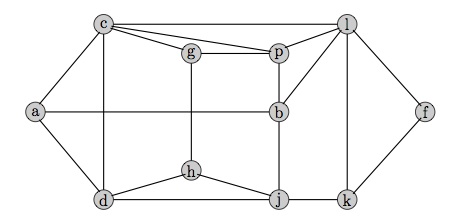
   1. (5 points) The set of feasible solutions to the node packing problem on a graph G = (V,E) with n vertices and m edges can be written as

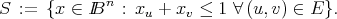
      We saw in class that the convex hull of S has dimension n and the nonnegativity constraints define facets of conv(S). Give another facet of conv(S) for the given graph.

   2. (5 points) Find a packing of cardinality 4 in the given graph.
   3. (10 points) Give a set of valid inequalities that together show that there cannot be a packing of cardinality greater than 4.
   4. (5 points) Is the graph perfect? (Justify your answer.)
   5. (7 points) Find nonnegative integral node weights c_v such that the optimal value of the LP relaxation

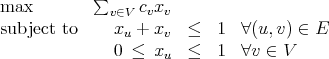
      is not integral.

   6. (8 points) The Lovasz Θ semidefinite programming relaxation of the node packing problem has dual problem

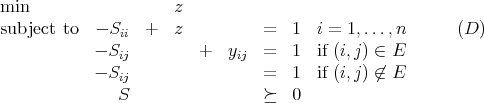
      Give a feasible solution to the dual problem with value 4.