Recall the following material on clustering problems from Homework 4:
Given the complete graph Kn =: (V,E) on n vertices, a clustering of the vertices is obtained by choosing an integer p and a partition of the vertices into p sets V 1,…,V p satisfying:
V s ∩ V t = ∅ for 1 ≤ s < t ≤ p and ∪s=1pV s = V .
Note that p is not fixed. The incidence vector of this clustering is defined by
Let Q be the set of incidence vectors of clusterings for Kn. Let edge (i,j) have weight wij. The clustering problem for this set of edge weights is then
The edge weights wij can be positive or negative. Valid triangle inequalities for this problem for three distinct vertices i, j, k are
Let U ⊆ V and let p = |U|. Assume p ≥ 5 and p is odd. Let E(U) be the edges with both endpoints in U. Let C ⊆ E(U) be a Hamiltonian tour through the vertices U. Denote the order of the vertices in the tour as i1 -i2 -…-ip -i1. Prove that the following constraint is valid for the clustering problem:
Solve the following binary knapsack problem using branch-and-bound:
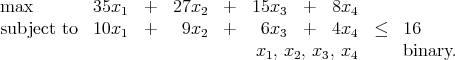
(Note: Linear programming relaxations of knapsack problems can be solved very easily. In particular, here the variables are ordered so that the ratios of the objective function coefficients ci to constraint coefficients ai satisfy
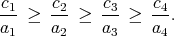
Then the solution is to take x1 as large as possible, then x2 as large as possible, then x3 as
large as possible, and then x4 as large as possible. For the initial LP relaxation, this gives a
solution of x = (1,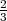 , 0, 0).
, 0, 0).
It may be useful to know that 0.7 × 35 = 24.5.)
The binary variables xi, i = 1,…, 4 satisfy
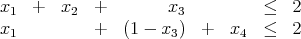
The constraint x2 + x4 ≤ 2 follows trivially from the upper bounds on the binary variables. By thinking of this as a constraint when x1 = 0, lift it to give a stronger valid constraint of the form
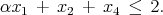
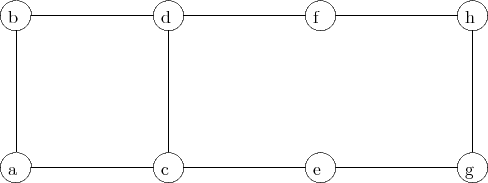
We want to solve the Max Cut problem on the graph G = (V,E) which has edge weights we. Part of the graph has the following structure:
Prove that the valid inequality
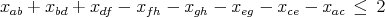
does not define a facet of the convex hull of the set of incidence vectors of cuts.
Let c and a be integral positive n-vectors and let b be a positive integer. The knapsack problem max{cT x : aT x ≤ b, x
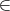 IBn} can be solved in time polynomial in n and b, yet the
knapsack problem is NP-Hard. Why is this not a contradiction?
IBn} can be solved in time polynomial in n and b, yet the
knapsack problem is NP-Hard. Why is this not a contradiction?