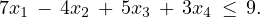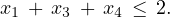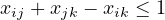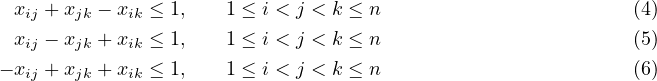In the examples below, x is required to be a nonnegative vector in ℝ³ and y is constrained to be a binary vector with three components. A set of constraints that must be satisfied by x and y is given, and a point that satisfies these constraints is also given. Find a valid flow cover inequality that cuts off this point.

1. Constraints:

   

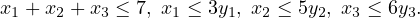
   Point:

   

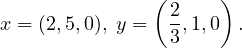
2. Constraints:

   

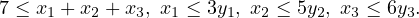
   Point:

   

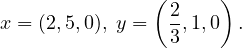
Let P = {x ∈ ℝⁿ : Ax ≤ b} and S = P ∩ Bⁿ. Let S⁰ := {x ∈ S : x₁ = 0}. Assume g^Tx ≤ h is a valid constraint for S⁰, and g₁ = 0. Let μ be the optimal value of the linear program max{g^Tx : x ∈ P,x₁ = 1}. Prove the following inequality is valid for S:

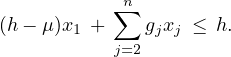
Let S be the set of binary variables x ∈ B⁴ satisfying

(1)

When x₂ = 1, we have the valid constraint

(2)

Lift the inequality to give a valid inequality for S. (Hint: consider a change of variables z₂ := 1 - x₂. Make sure you convert your constraint back to the x variables.)

Let

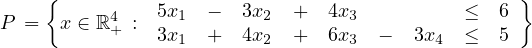
and S = P ∩ B⁴. The point 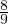x = (,0,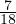,0) ∈ P, but it is not in the convex hull of S. Exploit the disjunction x₁ + x₃ ≤ 1 or x₁ + x₃ ≥ 2 to find a valid constraint for S that is violated by x.

Let S denote the set of feasible solutions to a clustering problem with n items, as discussed in Lecture 12D. Show that the triangle inequality

(3)

defines a facet of conv(S) for 1 ≤ i < j < k ≤ n.

Choose a seed and solve the clustering problem in

http://www.rpi.edu/~mitchj/matp6620/hw4html/clr1.mod

using a cutting plane algorithm, solving LP relaxations and adding violated triangle inequalities of the forms

Note: The AMPL file is designed to create a clustering problem with certain properties. If you use a different software package to solve this question, then you need to make sure you generate a clustering problem of the same form as that described in the AMPL file.