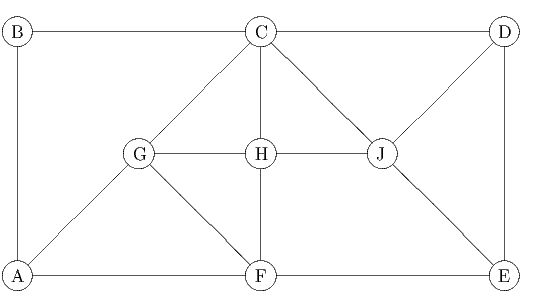
The following graph G = (V,E) is used in question 1.

1. Consider a matching problem on the graph above. The LP relaxation consists of nonnegativity together with the constraints ∑ _e∈δ(v)x_e ≤ 1 for each vertex v. A feasible solution to the LP relaxation is to take x_AB = 0.5, x_AF = 0, x_AG = 0.5, x_BC = 0.5, x_CD = 0, x_CG = 0, x_CH = 0.4, x_CJ = 0.1, x_DE = 0.2, x_DJ = 0.8, x_EF = 0.8, x_EJ = 0, x_FH = 0.2, x_GH = 0.4, and x_HJ = 0.
   1. Find a valid constraint for the matching problem that is violated by this solution.
   2. Assume the six diagonal edges each have weight two and the remaining 10 edges each have weight one. What is the maximum weight matching? Prove your solution is optimal.
2. The optimal tableau to the linear programming relaxation of the integer program given in Question 5 on Homework 2 is

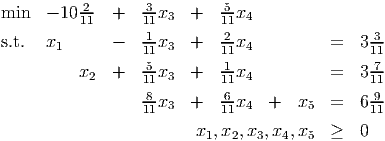
   where x₃, x₄ and x₅ are the slack variables in the three constraints. Find the Gomory and strong Gomory cutting planes implied by the three constraints. Express these constraints in terms of the original variables x₁ and x₂ and draw them on a graph of the feasible region.

3. A particular graph G = (V,E) consists of six vertices. Vertices 1–5 form a cycle and vertex 6 is adjacent to three of the other vertices. Any node packing on this graph must satisfy the odd hole inequality

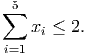
   How does the structure of the edges connecting vertex 6 to the rest of the graph affect the lifted odd hole inequality

   

4. Let G = (V,E) be a complete graph with five vertices with edge lengths c_e given in Table 1.

   ---

   	v1	v2	v3	v4	v5
   v1	—	3	7	2	8
   v2	—	—	2	9	8
   v3	—	—	—	7	1
   v4	—	—	—	—	2
   v5	—	—	—	—	—

   
   

   Table 1: Edge lengths for Question 4

   ---

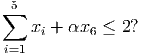
   We want to solve the MAXCUT problem on this graph. In this problem, the vertices are partitioned into two sets with the objective of maximizing the total weight of the edges with one endpoint in each set. This can be modeled as an integer programming problem by introducing binary variables x_e to indicate whether an edge is in the cut.

   Take the unit box as the initial LP relaxation. Solve this problem by using the following two-step procedure:

   • Solve the LP relaxation
   • If necessary, add one or more of the inequalities corresponding to cycles of length 3 that are violated by the solution to the LP relaxation, namely:

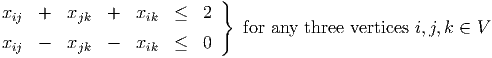
   and repeating. Write down the cuts violated at each iteration. You should only need to add one constraint of the second type. (You may want to use AMPL or a similar package to solve the LP relaxations. See the course webpage for details on how to use AMPL. If you need more help, see me. The initial AMPL model and data file are in

   http://www.rpi.edu/~mitchj/matp6620/hw3html/hw3q4.mod
   http://www.rpi.edu/~mitchj/matp6620/hw3html/hw3q4.dat

   respectively.)

5. Let G = (V,E) be a complete graph. Let C be a cycle of length 4 with edges e,f,g,h. A valid inequality is

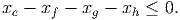
   Show that this inequality is implied by two inequalities corresponding to cycles of length 3.

6. The Project:
   Along with your solutions to this homework, hand in a brief description of what you would like to do for the project part of this course.