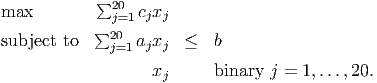
Due: Tuesday, January 24, 2023, by end of day, on LMS.
Penalty for late homeworks: 10% for each day or part of a day.
Questions 1–5 of this homework are concerned with a knapsack problem with 20 objects,
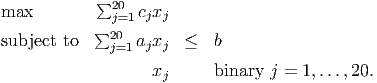
A link to the data can be found in question 1 of the online version of this homework. In your initial formulation use variables xj to indicate whether object j is used.
You will solve this problem using AMPL and CPLEX. The packages are available on LMS. More on these packages can be found at http://www.rpi.edu/~mitchj/ampldetails.html and also on LMS.
I lectured about AMPL in MATP 4700, and the videos are linked in LMS, and also available on Box from following the link on the webpage for that course, http://homepages.rpi.edu/~mitchj/matp4700/ (see Lecture 9C).
Part 1: introduction (14:17). Link: https://rensselaer.webex.com/webappng/sites/rensselaer/recording/play/3602c4e8d6cc489e994d7e176dd425bb
Part 2: an example session. Note: You may want to play this lecture full-screen. (22:03). Link: https://rensselaer.webex.com/webappng/sites/rensselaer/recording/play/e0f03ef357db4444ada1977df3c143e6
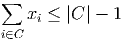
for subsets C ⊆{1,…, 20}, where ∑ j∈Caj > b. The ampl code for cover constraints is included in the model file, along with one commented-out line in the data file.
subject to cover3{i in 1..n-2, j in i+1..n-1, k in j+1..n}:
x[i] + x[j] + x[k] <= 2;
Given a graph G = (V,E), does there exist a partition of the edges E into two sets E1 and E2 such that neither E1 nor E2 contains a triangle?
Can you find a feasible solution to the LP relaxation of your formulation?
| John Mitchell |
| Amos Eaton 325 |
| x6915. |
| mitchj at rpi dot edu |
| Office hours: Tuesday 2-4pm in AE 325 (masks required), |
| and Thursday 3pm–4pm on webex: https://rensselaer.webex.com/meet/mitchj |