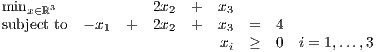
MATP 4700 Math Models of Operations Research
Homework 7
This homework will not be collected or graded.
The first three questions concern the following linear program
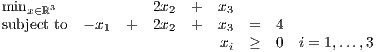 | (1) |
which has dual problem
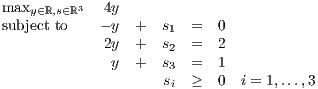 | (2) |
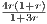 . Show that x(r) := (4r,1 + r,2 + 2r) solves the barrier problem
. Show that x(r) := (4r,1 + r,2 + 2r) solves the barrier problem
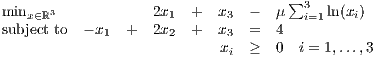 | (3) |
for any r > 0. (Hint: this is equivalent to showing that x(r) is on the central path. You need to find dual feasible (y(r),s(r)) so that (x(r),y(r),s(r)) satisfy the central path conditions.) (Lecture 25)
In addition, read Sections 1.8, 21.1 and 7.8 from the text.
Solving the homework problems (and other problems from the text) will improve your understanding of the material.
Working out the problems yourself will greatly improve your understanding of the material and help you on the exams. You can ask questions on piazza, in addition to using office hours or email.
Exam 3 will be on Friday December 8 and will cover integer programming, interior point methods, and dynamic programming. There is no final exam.
| John Mitchell, mitchj at rpi dot edu |
| Amos Eaton 325. x6915. |
| Office hours: |
| Tuesdays 2.30–4pm in AE 325; |
| Thursdays 1–3pm webex: https://rensselaer.webex.com/meet/mitchj |
| TA: Marguerite Demasi, demasm at rpi dot edu |
| Office hours: Mondays 2–3.30pm in AE 317. |