Questions from Kupferschmid, Chapter 7 (available on LMS):

• 7.10.16 (a): Lecture 21. Note: The solution x_LP^* to the LP relaxation is given in the picture on page 261. When you branch, you can solve 2-dimensional subproblems, so you can solve the subproblems graphically. For example, when solving the branch with x₁ ≥ 2, the solution to the relaxation will have x₁ = 2, so you can solve a problem in just x₂ and x₃; if you branch further (eg, on x₃ ≥ 1), then you have to unfix x₁ and set x₃ = 1 in the LP relaxation.
• 7.10.37: Lecture 22. Make sure your constraint is linear! Further, consider the set of valid inequalities x₁ ≤ x₂ together with x₁ ≤ x₃; show that the set of inequalities is stronger than the single inequality, in that there are fractional points that satisfy the single inequality but are violated by at least one of the set of two inequalities.
• 7.10.39 (a): Lecture 22. Note: requiring that the “difference as small as possible” means that we want the absolute value of the difference of the 2 numbers to be as small as possible.
• 7.10.43: Lecture 22. Note: You don’t need to consult the cited reference [73].
• Gomory: Lecture 23. The LP relaxation of an integer program has optimal tableau

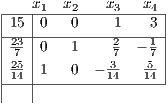
  a.

  Derive a Gomory cutting plane from each constraint and verify that it is violated by the solution to the current LP relaxation.

  b.

  Add the Gomory cut corresponding to the second constraint and reoptimize. What do you conclude?

In addition, read Sections 7.1–7.7 from the text.

Solving the homework problems (and other problems from the text) will improve your understanding of the material.

Working out the problems yourself will greatly improve your understanding of the material and help you on the exams.

You can ask questions on piazza, in addition to using office hours or email.