Due: Monday, June 8, 2020, 11.59pm.
Answer the following questions. Upload your solutions as a single pdf file to LMS. Include your
last name and HW1 in the name of the file, eg, mitchellHW1.pdf. No late homework
accepted.
- Section 15.4, pages 863–866:
- Let the domain
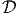 = {(x,y) : x ≥ 0, x2 + y2 ≤ 4}. Find ∫ ∫
= {(x,y) : x ≥ 0, x2 + y2 ≤ 4}. Find ∫ ∫
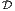 xy dxdy using polar
coordinates.
xy dxdy using polar
coordinates.
- Find ∫
02 ∫
x2xy dy dx using polar coordinates. (Hint: the integral of 1∕ cos 2(θ) is
tan(θ).)
- Let the domain
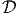 = {(r,θ) : 0 ≤ θ ≤ π∕2, 0 ≤ r ≤
= {(r,θ) : 0 ≤ θ ≤ π∕2, 0 ≤ r ≤ 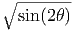 }. Find
∫
∫
}. Find
∫
∫
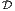 x
x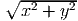 dxdy using polar coordinates. (Hint: use double angle formula and
also the identity sin 2θ + cos 2θ = 1.
dxdy using polar coordinates. (Hint: use double angle formula and
also the identity sin 2θ + cos 2θ = 1.
- Use cyclindrical coordinates to integrate f(x,y,z) = z
 over the domain
over the domain
 = {(x,y,z) : x2 + y2 ≤ z ≤ 2 - x2 - y2}.
= {(x,y,z) : x2 + y2 ≤ z ≤ 2 - x2 - y2}.
- Use spherical coordinates to integrate f(x,y,z) = z over the domain
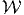 =
{(x,y,z) : x2 + y2 + z2 ≤ 4z, z ≥
=
{(x,y,z) : x2 + y2 + z2 ≤ 4z, z ≥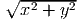 }.
}.
- Section 15.5, pages 874–878:
- Find the total population within a 4-km radius of the origin with x ≥ 0, y ≥ 0,
with population density 2000(x2 + y2)-0.3. (Hint: use polar coordinates.)
- Find the centroid of the infinite lamina with x ≥ 1 and 0 ≤ y ≤ x-3 with density
δ(x,y) = 1.
- Find the centroid of
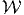 = {(x,y,z) : x,y,z ≥ 0, x∕R + z∕H ≤ 1, x2 + y2 ≤ R2}
for positive parameters R and H. (Hint: use cylindrical coordinates and double
angle formulas.)
= {(x,y,z) : x,y,z ≥ 0, x∕R + z∕H ≤ 1, x2 + y2 ≤ R2}
for positive parameters R and H. (Hint: use cylindrical coordinates and double
angle formulas.)
- Let
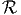 be infinite lamina with x ≥ 0 and y ≥ 0 and with density δ(x,y) = e-x-y.
Find the moments of inertia Ix and Iy.
be infinite lamina with x ≥ 0 and y ≥ 0 and with density δ(x,y) = e-x-y.
Find the moments of inertia Ix and Iy.
- The random variables x and y have domain
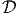 = {(x,y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 -x}and
probability density p(x,y) = Cxy on
= {(x,y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 -x}and
probability density p(x,y) = Cxy on 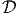 for some positive constant C.
for some positive constant C.
- Determine C so that p(x,y) is a probability density on
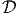 .
.
- What is the probability that x ≥ 2y?
Homework submission guidelines
Submissions: you can make multiple submissions of a homework, but only the final
submission will be graded. The single pdf file submitted will be a multipage document, and the
pages must be in the correct order.
Producing a pdf file: the homework assignments will involve extensive mathematical
formulas and expressions, and will often require sketches (of curves, domains, etc).
- Suggestion 1 (free):
a) write out the solutions neatly, and clearly, on regular paper
b) use a pdf scanner on your phone, and produce one multipage pdf file. Recommended
scanning apps include Adobe Scan (highly recommended), ABBYY FineScanner,
CamScanner
- Suggestion 2 (not free):
use an iPad, or something similar, along with a pdf producing note taking app (like
Notability)
- Suggestion 3 (free):
use LaTeX. This produces easy to read text but doing sketches is more complicated.
The reason is that you will need to make pdf images of your sketches, and then include
them in the LaTeX output. This is not difficult to do, and if you want to try this just
ask and we will provide more information on what to do.
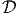 = {(x,y) : x ≥ 0, x2 + y2 ≤ 4}. Find ∫ ∫
= {(x,y) : x ≥ 0, x2 + y2 ≤ 4}. Find ∫ ∫
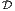 xy dxdy using polar
coordinates.
xy dxdy using polar
coordinates.
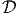 = {(r,θ) : 0 ≤ θ ≤ π∕2, 0 ≤ r ≤
= {(r,θ) : 0 ≤ θ ≤ π∕2, 0 ≤ r ≤ 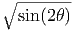 }. Find
∫
∫
}. Find
∫
∫
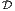 x
x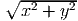 dxdy using polar coordinates. (Hint: use double angle formula and
also the identity sin 2θ + cos 2θ = 1.
dxdy using polar coordinates. (Hint: use double angle formula and
also the identity sin 2θ + cos 2θ = 1.
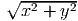 over the domain
over the domain
 = {(x,y,z) : x2 + y2 ≤ z ≤ 2 - x2 - y2}.
= {(x,y,z) : x2 + y2 ≤ z ≤ 2 - x2 - y2}.
 =
{(x,y,z) : x2 + y2 + z2 ≤ 4z, z ≥
=
{(x,y,z) : x2 + y2 + z2 ≤ 4z, z ≥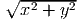 }.
}.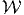 = {(x,y,z) : x,y,z ≥ 0, x∕R + z∕H ≤ 1, x2 + y2 ≤ R2}
for positive parameters R and H. (Hint: use cylindrical coordinates and double
angle formulas.)
= {(x,y,z) : x,y,z ≥ 0, x∕R + z∕H ≤ 1, x2 + y2 ≤ R2}
for positive parameters R and H. (Hint: use cylindrical coordinates and double
angle formulas.)
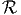 be infinite lamina with x ≥ 0 and y ≥ 0 and with density δ(x,y) = e-x-y.
Find the moments of inertia Ix and Iy.
be infinite lamina with x ≥ 0 and y ≥ 0 and with density δ(x,y) = e-x-y.
Find the moments of inertia Ix and Iy.
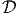 = {(x,y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 -x}and
probability density p(x,y) = Cxy on
= {(x,y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 -x}and
probability density p(x,y) = Cxy on 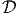 for some positive constant C.
for some positive constant C.
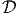 .
.