Due: Thursday, June 4, 2020, 11.59pm.
Answer the following questions. Upload your solutions as a single pdf file to LMS. Include your
last name and HW1 in the name of the file, eg, mitchellHW1.pdf. No late homework
accepted.
- Section 15.1, pages 829–832:
- Let R = [0, 1] × [0, 2]. Find ∫
∫
Re2x+3ydxdy.
- Let R = [1, 2] × [2, 3]. Find ∫
∫
Rx2y dxdy.
- Let R = [0, 1] × [0, 2]. Find ∫
∫
Rxexydxdy. (Hint: think about the order of
integration.)
- Section 15.2, pages 841–845:
- Integrate f(x,y) = (x + y + 1)-2 over the triangle with vertices (0, 0), (0, 3), and
(3, 0).
- Integrate f(x,y) = cos(2x + y) over the domain
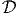 = {(x,y) : 0 ≤ x ≤
= {(x,y) : 0 ≤ x ≤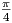 , 0 ≤
y ≤ 2x}.
, 0 ≤
y ≤ 2x}.
- Sketch the domain of integration of ∫
01 ∫
exef(x,y)dy dx and express as an iterated
integral in the opposite order.
- Let
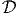 be the quadrilateral satisfying 1 ≤ y ≤ 2 and
be the quadrilateral satisfying 1 ≤ y ≤ 2 and 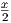 ≤ y ≤ x. Calculate the
integral of f(x,y) =
≤ y ≤ x. Calculate the
integral of f(x,y) = 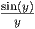 over
over 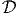 . (Hint: think about the order of integration.)
. (Hint: think about the order of integration.)
- Section 15.3, pages 854–856:
- Integrate f(x,y) = y over the domain
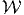 = {(x,y,z) : x2 + y2 ≤ z ≤ 4}.
= {(x,y,z) : x2 + y2 ≤ z ≤ 4}.
- Let
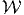 be the region in the first quadrant {x ≥ 0,y ≥ 0,z ≥ 0} that lies below
the paraboloid x2 + y2 = z - 2 and above the plane x + y + z = 2. Express
∫
∫
∫
be the region in the first quadrant {x ≥ 0,y ≥ 0,z ≥ 0} that lies below
the paraboloid x2 + y2 = z - 2 and above the plane x + y + z = 2. Express
∫
∫
∫
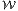 f(x,y,z) dV as an iterated integral.
f(x,y,z) dV as an iterated integral.
- Section 15.4, pages 863–866: Express the region
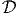 in Question 2d in polar coordinates.
(You are not required to find the integral in polar coordinates.)
in Question 2d in polar coordinates.
(You are not required to find the integral in polar coordinates.)
Homework submission guidelines
Submissions: you can make multiple submissions of a homework, but only the final
submission will be graded. The single pdf file submitted will be a multipage document, and the
pages must be in the correct order.
Producing a pdf file: the homework assignments will involve extensive mathematical
formulas and expressions, and will often require sketches (of curves, domains, etc).
- Suggestion 1 (free):
a) write out the solutions neatly, and clearly, on regular paper
b) use a pdf scanner on your phone, and produce one multipage pdf file. Recommended
scanning apps include Adobe Scan (highly recommended), ABBYY FineScanner,
CamScanner
- Suggestion 2 (not free):
use an iPad, or something similar, along with a pdf producing note taking app (like
Notability)
- Suggestion 3 (free):
use LaTeX. This produces easy to read text but doing sketches is more complicated.
The reason is that you will need to make pdf images of your sketches, and then include
them in the LaTeX output. This is not difficult to do, and if you want to try this just
ask and we will provide more information on what to do. Again, there is to be only
one pdf file submitted per assignment.
| John Mitchell |
| Amos Eaton 325 |
| x6915. |
| mitchj at rpi dot edu |
| Office hours: Mon, Tues, Thurs, Fri: 2.30–3.30pm, WebEx. |
| |
| TA: Rachel Wesley. |
| Office hours: available on Slack and WebEx. |
| WebEx time: Mon, Thurs 11am-noon, wesler; or by appointment. |
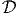 = {(x,y) : 0 ≤ x ≤
= {(x,y) : 0 ≤ x ≤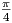 , 0 ≤
y ≤ 2x}.
, 0 ≤
y ≤ 2x}.
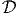 be the quadrilateral satisfying 1 ≤ y ≤ 2 and
be the quadrilateral satisfying 1 ≤ y ≤ 2 and 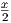 ≤ y ≤ x. Calculate the
integral of f(x,y) =
≤ y ≤ x. Calculate the
integral of f(x,y) = 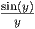 over
over 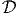 . (Hint: think about the order of integration.)
. (Hint: think about the order of integration.)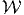 = {(x,y,z) : x2 + y2 ≤ z ≤ 4}.
= {(x,y,z) : x2 + y2 ≤ z ≤ 4}.
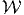 be the region in the first quadrant {x ≥ 0,y ≥ 0,z ≥ 0} that lies below
the paraboloid x2 + y2 = z - 2 and above the plane x + y + z = 2. Express
∫
∫
∫
be the region in the first quadrant {x ≥ 0,y ≥ 0,z ≥ 0} that lies below
the paraboloid x2 + y2 = z - 2 and above the plane x + y + z = 2. Express
∫
∫
∫
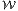 f(x,y,z) dV as an iterated integral.
f(x,y,z) dV as an iterated integral.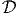 in Question 2d in polar coordinates.
(You are not required to find the integral in polar coordinates.)
in Question 2d in polar coordinates.
(You are not required to find the integral in polar coordinates.)